大数据量下的机器学习
现在的数据量越来越大,也有着很多的机器学习算法在不断优化来适用于大数据的情况。由于数据量很大,其实一个简单的机器学习算法,在偏差(bias)不大的情况下都会有很高的准确率。所以目前是更加倾向于加大训练集的大小来提高预测的准确率。然而随着训练集的加大,很多像梯度下降这样的算法的计算速度会越来越慢,因此要提出一些措施来提高算法的性能。
对于梯度下降算法:
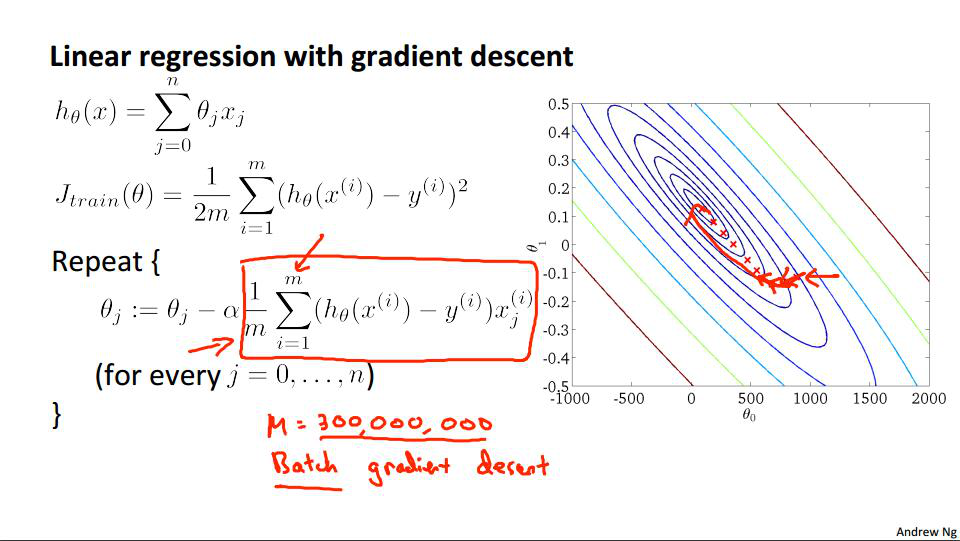
由于在每次迭代中都要计算红色方框中的这个步骤,而这个是要遍历所有的样本进行计算,所以在样本数量特别大的情况下,每次迭代都会耗掉非常多的时间,并且对于最后结果来讲仅仅是进行了一次迭代而已,所以在数据量很大的情况下用原始的梯度下降算法(Batch Gradient Descent)效果很不理想。
随机梯度下降
将原始的梯度下降算法的cost function改写后可以变成下面这个形式:
\[J_{train}(\theta) = \dfrac{1}{m} \displaystyle \sum_{i=1}^m cost(\theta, (x^{(i)}, y^{(i)}))\] \[cost(\theta,(x^{(i)}, y^{(i)})) = \dfrac{1}{2}(h_{\theta}(x^{(i)}) - y^{(i)})^2\]现在$J_{train}$可以想象成是在当时那次迭代的$\theta$下,每个样本误差的累加后的平均,所以可以在随机打乱样本顺序之后,按照下面的迭代来处理随机下降算法:
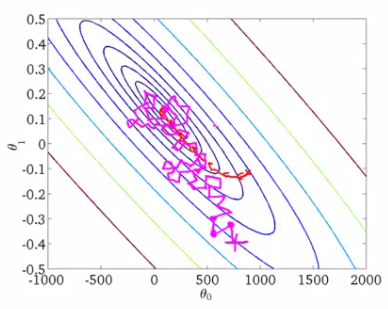
\[\Theta_j := \Theta_j - \alpha (h_{\Theta}(x^{(i)}) - y^{(i)}) \cdot x^{(i)}_j\]这个算法每次迭代只考虑一个样本,不需要像之前那样讲所有的样本累加起来计算一个导数项,所以速度上会比之前的梯度下降算法快很多,然而由于只考虑了一个样本,所以每次迭代的方向可能会很奇怪,不一定是向着全局最优解的方向收敛过去的,每一步之后cost function的值可能会增大,最后也不是停在全局最优解的位置,而是在那个位置附近不断的震荡,震荡的范围取决于步进速率$\alpha$的大小。
在图形上比较直观的结果是类似这样:
由于现在的电脑有多核或者如果采用分布式的方式计算,在向量化处理的很好的情况下,由于一次可以计算多个值,所以采用一种叫做Mini-batch Gradient Descent的算法来处理效率会更高。
这种算法是介于梯度下降算法和随机梯度下降算法之间的一种方式,有点像综合了两个算法,每次选取一定量的训练样本进行迭代,这样做有类似于随机梯度下降的好处,不需要每次迭代遍历所有的样本,所以速度会比梯度下降快,并且向量化处理得好的话,每次迭代可以处理这一批样本的计算,基本类似随机梯度下降一次的计算时间,并且由于迭代次数比随机梯度下降少很多,所以这个算法的计算速度往往是最快的。不过对于每次迭代中样本的数量需要不断的尝试,所以这个算法又多出了一个参数,作者推荐的是一次迭代10个样本,不过一般来讲,这个数字在2到100之间都是合理的。
然后针对下降速率$\alpha$,如果$\alpha$选取过大,会造成不收敛甚至发散,过小会导致收敛很慢,所以有一个做法是随着迭代次数增加,$\alpha$逐渐减小。通常让$\alpha$满足这个公式:
\[\alpha = \dfrac{const1}{iterationNumber + const2}\]但是通常人们不愿意这么做,原因是要不断的尝试这里的两个参数const1和const2。
随机梯度下降算法收敛
判断随机梯度下降算法是否收敛的方法与之前一样,也是观察cost function随着迭代次数变化的图像,但是由于这个算法里面不是每次都朝着正确的方向迭代,所以会有很多噪声。并且由于数据量很大,往往不会每次迭代都会输出目前cost function的值,现在观察几种不同情况下收敛情况
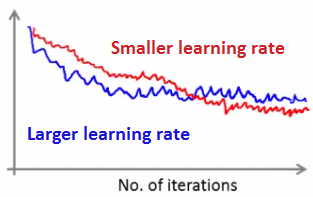
学习速率对结果的影响:
往往学习速率较小,后面的迭代在全局最优解附近震荡的范围越小,结果也就越好,这时候图像类似于这样:
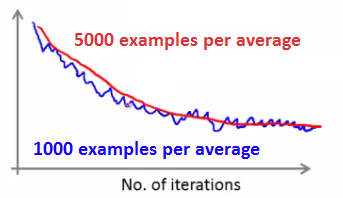
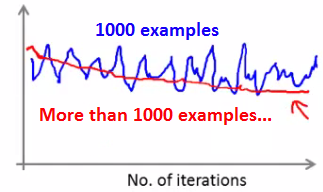
每次输出平均值时样本的数量:
由于每次输出会发现明显的震荡,而迭代了100次才输出一次图像的情况下,图像会显得更加平滑,这时可能更容易看出整体的走势:
在线学习(Online Learning)
如果有一个推荐网站,由于不断有用户在使用这个网站,可以不断的获得新的训练样本,所以可以采取类似于随机梯度下降的方式,每次针对当前样本进行训练,训练结束之后就直接抛弃这个样本继续拿下一个样本进行训练,这样做的好处是首先不需要储存这些训练样本,可以节省磁盘空间,并且由于数据量不断,所以舍弃之前已经训练过的样本其实影响不大。其次,如果未来用户的口味改变了,这种方式训练的模型使可以适应新的用户类型的,而之前的训练样本已经不适用于这个时代了,不应该重新拿之前的数据来训练。这在网站的推荐系统中还比较重要,这个算法可以随着用户口味的变化来调整模型的参数。
Map Reduce and Data Parallelism
再回来看之前的梯度下降算法,每次迭代中都有遍历所有样本,将预测误差累加起来的步骤,这些步骤中每次加法都是跟$\Theta$和需要相加的样本有关,所以可以考虑将样本分成很多分,针对每部分样本,计算
\[\displaystyle \sum_{i=p}^{q}(h_{\theta}(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)}\]其中p为样本起始序号,q为最后一个样本的序号。这个结果存在一个临时变量$temp_j$中,最后针对每个电脑,将计算结果按照这个公式综合一下,每次迭代就可以写成下面这个形式:
\[\Theta_j := \Theta_j - \alpha \dfrac{1}{z}(temp_j^{(1)} + temp_j^{(2)} + \cdots + temp_j^{(z)})\]其中的每个$temp_j$都是可以分给不同电脑来计算的,最后由一个电脑计算出这次迭代后的$\Theta$送给每台电脑进行下一个迭代的计算。
这种平行化的计算由于缩短了每次迭代的时间,所以能提高算法的性能。不仅是针对分布式计算机群,对于只有一台电脑的情况,由于现在电脑有时候有多个CPU,每个CPU又会有多个核,所以也可以采用这种方式让电脑进行并行计算,但是需要注意的是,如果在算法中使用了一些线性代数库的话,有些库可能已经考虑了并行计算并且处理的很好,调用相关的函数会自动使用并行计算,这时候就不用再考虑这个方式了,只需要看自己代码中向量化有没有处理好就行了。
不光是梯度下降算法,对于神经网络有时候也是可以把正向传播和反向传播交给其他计算机处理,然后汇总处理结果进行迭代。总的来说,只要机器学习算法可以写成训练集中函数的计算和的这种形式,都是可以考虑使用Map Reduce这种方法来进行数据的平行花计算的。
参考
所有笔记链接
- [笔记]0.machine-learning-第0篇笔记
- [笔记]1.machine-learning-介绍
- [笔记]2.machine-learning-多元线性回归
- [笔记]3.machine-learning-分类
- [笔记]4.machine-learning-神经网络
- [笔记]5.machine-learning-成本函数和反向传播算法
- [笔记]6.machine-learning-应用机器学习的建议
- [笔记]7.machine-learning-支持向量机
- [笔记]8.machine-learning-分类
- [笔记]9.machine-learning-异常检测
- [笔记]10.machine-learning-大数据量下的梯度下降算法
- [笔记]11.machine-learning-应用示例:照片中的光学字符识别
