动机
线性回归和逻辑回归能解决许多的机器学习问题,然而当feature过多并且feature之间相互影响的情况下,无法通过构建线性模型处理问题。
考虑房价的预测问题,如果房屋的价格只与面积和卧室数量有关的话并且这两个feature之间并没有相互影响,我们可以得到类似于
\[h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + ......\]这样的形式,后面也许会根据情况加上$x_1$和$x_2$的高次项,这种情况在feature足够少的情况下不会出现什么问题,处理的结果应该也是可以接受的。但是当feature过多的时候问题会变得很麻烦,比如房屋价格还会考虑到楼层、房屋年限、邻居和周围环境等,并且这些feature往往会相互影响,假设有100个feature,最后会写出一个类似于这样的假设模型:
\[h_\theta(x) = g(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1 x_2 + \theta_4 x_1^2 x_2 + ... )\]光是feature的排列组合就会非常复杂。
也许房价的例子还不能看出feature之间的相互影响,通过图像识别更容易直观的感受神经网络的必要性。
假设有一个50 * 50像素的图片,要判断这个图片是不是表示的汽车,我们需要提取图像中所有的像素点,单个像素点单独判断并没有任何意义,这些像素点之间的相互排列才构成了一整幅图像。以这样的图片为例,就算是灰度图片也会有2500个feature,然后考虑两两组合,这时候使用线性模型会导致计算量过大。因此在复杂的非线性分类问题中一般采用神经网络的方法来处理。
神经网络方法是一个很古老的方法了,兴起于二十世纪八九十年代,但是由于计算量的问题当时的机器并不能满足这个算法,所以在90年代后期这个应用减少了。最近神经网络这个方法又逐渐热门起来了,其中一个原因是神经网络是计算量有些偏大的算法,然而近些年计算机的运行速度变快,才足以真正运行起大规模的神经网络。我个人认为机器学习是教会机器一些有规律的事情,当机器学习发展到一定阶段后能使用一套程序在电脑上模拟出人类的大脑,毕竟我们开始学习的时候也是只使用了一个大脑,没有在吃饭的时候调用一个程序,玩游戏的时候调用另一个程序。并且现在已经有实验室研究出了通过机器学习的方式来打游戏的方法,并且得分往往不低,有些实验室就是使用的一套程序。虽然目前通过这个方式能玩的游戏非常有限,并且这些游戏还比较简单,但是机器学习的前景是非常乐观的。
我觉得神经网络和其他机器学习方法的区别在于feature之间的关联关系,神经网络是通过一层层的节点相互作用来描述耦合的,这个方式更加像人类大脑的认知方式,但是目前很多模型我好像都看不出来实际表示的意义,就像是一个黑匣子,通过这个模型预测的结果似乎正确率很高,但是又不太说得出来一个有说服力的理由。并且神经网络的架构也像是一个感觉,需要设计的人有一定的直觉,直觉好一般能少走很多的弯路,这一点上又很像是艺术。
模型表示(Model Representation)
神经网络的模型一般是由输入层、隐藏层和输出层组成的。输入层是数据中获取的feature,比如房屋的面积、房间数量等,一个feature对应输入层的一个节点,这些feature之间的耦合关系是在隐藏层中体现出来的,隐藏层中的一个节点往往对应于输入层或者上一级隐藏层中的多个节点,也就是说这个节点的值受到多个feature的影响。很直观的表示是把这个类比为人类的大脑,每个神经网络中的节点都看作是神经元,神经元之间通过电信号传递消息,信息的传递是单向的。输入层就是外界对大脑的刺激,经过无数神经元的传递到达输出层,这时人才获取到相关的资讯。
模型的一个表示是:
\[\begin{bmatrix}x_0 \newline x_1 \newline x_2 \newline \end{bmatrix}\rightarrow\begin{bmatrix}\ \ \ \newline \end{bmatrix}\rightarrow h_\theta(x)\]中间的矩阵表示隐藏层,隐藏层可能不只有一层。神经网络中的具体任务应该就是设计出节点之间的连接关系,然后训练出具体的参数$\Theta$。
以一个有一层中间层的神经网络为例,模型架构为:
\[\begin{bmatrix}x_0 \newline x_1 \newline x_2 \newline x_3\end{bmatrix}\rightarrow\begin{bmatrix}a_1^{(2)} \newline a_2^{(2)} \newline a_3^{(2)} \newline \end{bmatrix}\rightarrow h_\theta(x)\]隐藏层的计算方式为:
\[\begin{align*} a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) \newline a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) \newline a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) \newline h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)}) \newline \end{align*}\]如果把$x = a^{(1)}$,就可以换一种方式写神经网络的模型:
\[\begin{align*} z^{(j)} = \Theta^{(j-1)}a^{(j-1)} \newline a^{(j)} = g(z^{(j)}) \newline h_\Theta(x) = a^{(j+1)} = g(z^{(j+1)}) \end{align*}\]实际应用
由于sigmoid函数一般是长这样
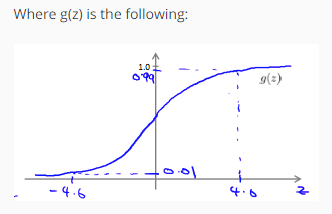
一般认为z大于4.6的时候函数值就近似为1了,当z小于 -4.6的时候函数值近似为0。
根据这个我们可以模拟出一些基础的操作:
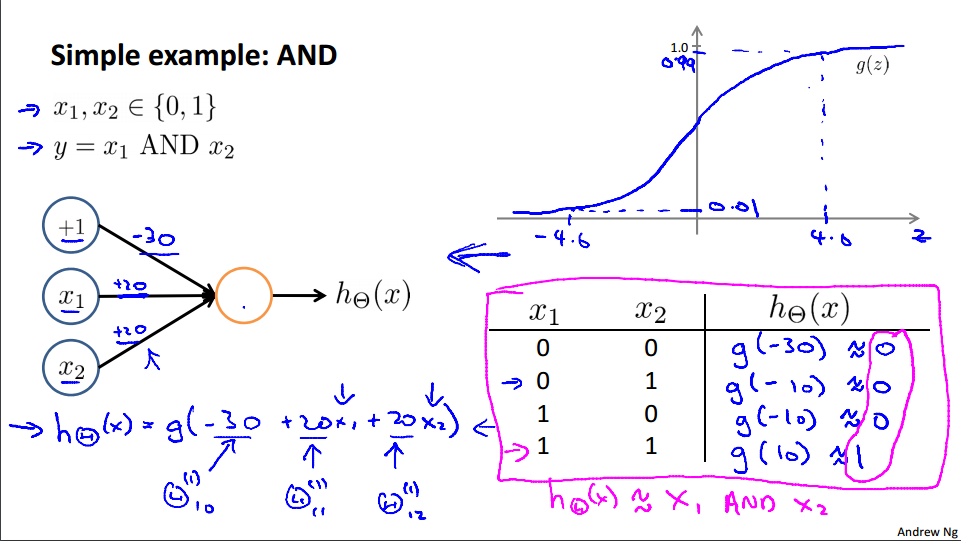
如上图的神经网络,可以画出真值表,用这个模型可以表示与门。类似的,可以画出下面这些神经网络:
OR:

Negation:
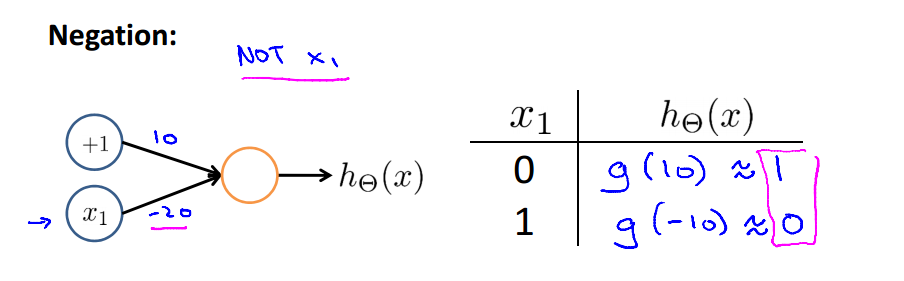
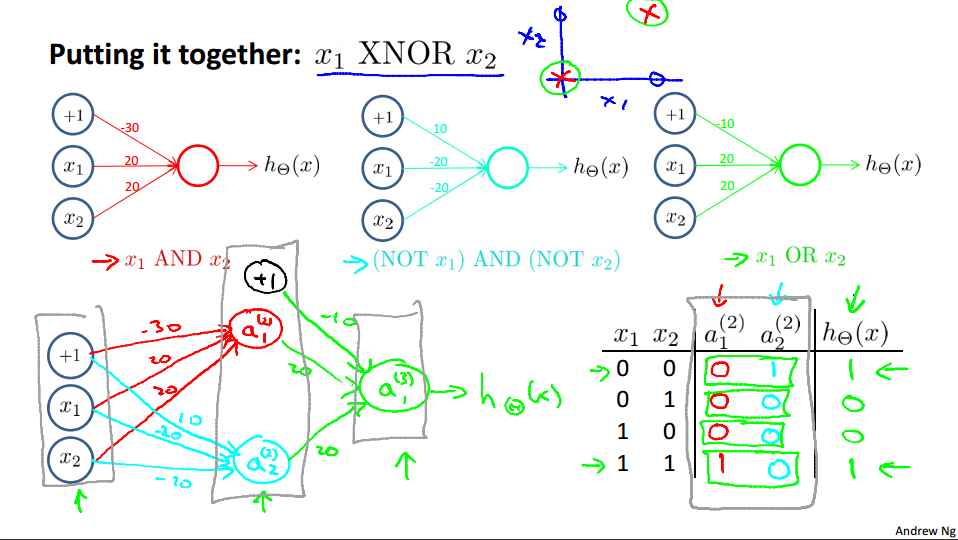
XNOR
参考
所有笔记链接
- [笔记]0.machine-learning-第0篇笔记
- [笔记]1.machine-learning-介绍
- [笔记]2.machine-learning-多元线性回归
- [笔记]3.machine-learning-分类
- [笔记]4.machine-learning-神经网络
- [笔记]5.machine-learning-成本函数和反向传播算法
- [笔记]6.machine-learning-应用机器学习的建议
- [笔记]7.machine-learning-支持向量机
- [笔记]8.machine-learning-分类
- [笔记]9.machine-learning-异常检测
- [笔记]10.machine-learning-大数据量下的梯度下降算法
- [笔记]11.machine-learning-应用示例:照片中的光学字符识别
