- 非监督学习介绍
- K-Means算法
- 优化目标(Optimization Objective)
- 随机初始化(Random Initialization)
- 选取集群数量K
- 维度下降(Dimensionality Reduction)
- 主成分分析(Principle Component Analysis(PCA))
- 选择压缩后的维度
- 运用PCA方法的建议
- 参考
- 所有笔记链接
非监督学习介绍
分类与之前的回归直观上最大的不同就是分类问题一般是没有给定的标签,而回归问题一般有大量给定正确标签的样本,可以把样本分为训练集验证集测试集什么的来得到一个足够好的模型。
K-Means算法
K-Means能将样本数据分成指定数量的集群,是目前为止使用的最多的分类算法
K-Means大概是先选取指定数量的中心,然后对所有的样本进行分群,看这个样本离哪个中心比较近,划分到最近的那个集群中,每一轮划分完成后,计算每个集群的中心,然后用新的中心替换原始的集群中心重复之前的步骤。
算法输入
K(需要分出来的群的数量)
样本集合($x^1, x^2, x^3, …, x^m$)
算法步骤
//随机初始化
Randomly initialize K cluster centroids mu(1), mu(2), ..., mu(K)
Repeat:
//将每个样本分到离最近的中心的那个集群
for i = 1 to m:
c(i):= index (from 1 to K) of cluster centroid closest to x(i)
//重新计算集群的中心
for k = 1 to K:
mu(k):= average (mean) of points assigned to cluster k
算法中$c^{(i)}$代表第i个样本分在哪一群,比如$c^{(5)} = 3$代表的意义是第5个样本被分在了第三个集群
mu(k)表示的是第k个集群的中心,数学公式表达为:$\mu_k = \dfrac{1}{n}[x^{(k_1)} + x^{(k_2)} + \dots + x^{(k_n)}] \in \mathbb{R}^n$
有可能在K-Means进行到中间某一次迭代的时候,有可能造成某一个群中没有样本,解决办法就是直接减少一个族群的数量,最后的结果是分成K - 1群,或者再随机初始化一个群出来
最后当运行一次迭代对分群造成的影响足够小的时候,K-Means方法就会收敛,这时候方法停止运行,或者在一般的API中,设置最大迭代次数方法也会停止运行。
优化目标(Optimization Objective)
K-Means方法的cost function定义为:
\[J(c^{(i)},\dots,c^{(m)},\mu_1,\dots,\mu_K) = \dfrac{1}{m}\sum_{i=1}^m ||x^{(i)} - \mu_{c^{(i)}}||^2\]其中:
- $c^{(i)}$ 表示第i个样本被分在哪一个群
- $\mu_k$ 表示第k群样本的中心
- $\mu_{c^{(i)}}$ 表示第i个样本所在的族群的中心
所以K-Means方法的优化目标就是使得cost function最小:
\[min_{c,\mu}\ J(c,\mu)\]这个成本函数又被称作是训练样本的失真,算法中每一次迭代的步骤实际上就是先固定$\mu_1,\dots,\mu_K$不变,调整$c^{(1)},\dots,c^{(m)}$使cost function最小,然后根据新的$c^{(1)},\dots,c^{(m)}$,重新计算$\mu_1,\dots,\mu_K$
随机初始化(Random Initialization)
在K-Means方法执行第一次迭代之前,会有一群初始的中心,不能挑同一个点作为好几个集群的中心,这样不能有效的运行K-Means,除非在后续的步骤中能区分出不同的集群然后很好的分开这些集群的中心,否则我感觉K-Means方法会完全失效。所以初始的集群中心一般是随机产生的,推荐的做法是从样本中随机挑选K的点,将这些点作为初始的集群中心,然后开始运行K-Means算法的后续步骤。
由于K-Means算法有可能落入一个局部最优解(这个跟随机初始化有关),所以在运用这个算法的时候一般会运行很多遍,每次计算cost function,然后选取cost function最小的那次的运行结果。
选取集群数量K
Elbow method
根据不同取值的K计算每次运行之后的cost function,然后画出cost function关于K变化的图像,加入运气比较好会出现这样的结果:
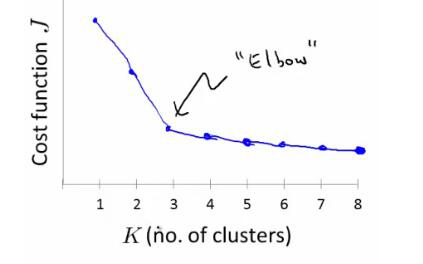
很明显在elbow之前,K增大对cost function的减小帮助是很大的,但是到了这个点之后,影响就会变得很小,所以权衡考虑会将K的取值选为肘部的这个点
但是很不幸的是,经常得到的这个曲线会很平缓的下降,没有明显的拐点,所以这个方法并不是一直都适用。
其他方法
根据经验判断,思考分群之后要拿这些数据去做什么,然后权衡成本和收益来判断到底该分成多少族群。
维度下降(Dimensionality Reduction)
维度下降是将高纬度的数据转化为低维度,这么做能减少样本中feature数量,加快算法运行的效率。并且有时候feature数量太多会造成混乱,很难从直觉上观察样本分类的情况,将数据降成3维或者2维的话就能使用工具做数据可视化操作,直觉上对数据的分布有一个印象,然后在后面的一些选择上面就不会有太多的弯路。
课程中给的一个例子是给定世界各地很多国家一些指标的数据集:
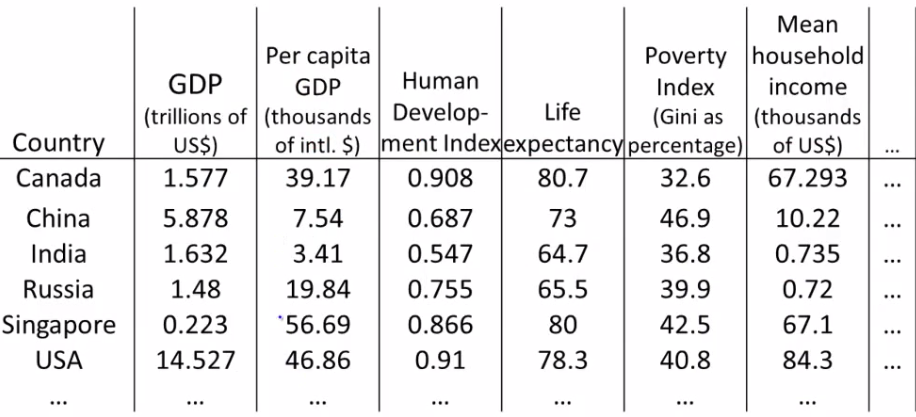
从这个表格中基本没办法直觉上分析这些数据,也不知道该怎么着手处理,如果通过维度下降,将这些数据变成二维的,可以将数据展示在平面中,然后能对数据整体有一个直观的感受了。
主成分分析(Principle Component Analysis(PCA))
PCA是一个很常用的维度下降算法,首先以二维的样本来举例,下面有五个散落在二维空间中的样本:
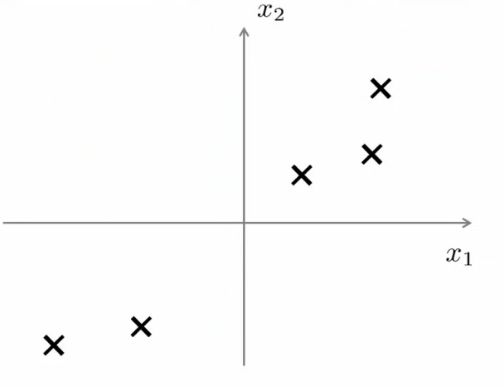
通过观察可以发现这些样本近似的分布在一条直线上,如果将这五个样本投影在这个直线上,直线上的投影点就能近似的代表这五个样本,也就达到了维度下降的目的(平面上的点投影到了线上),但是这条线的选择不同会对最后的分群结果产生不一样的影响,像下面这张图中红色的这根线,投影之后在分群应该和投影之前的结果基本是一样的
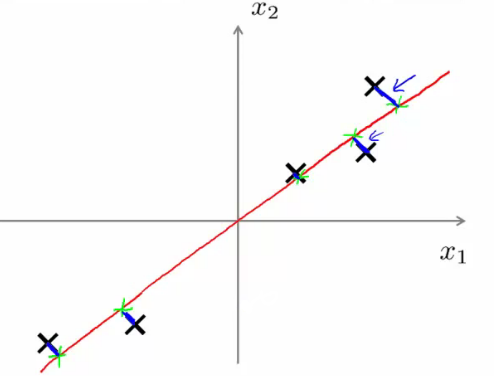
但是如果选取跟这条线垂直的线,会导致投影之后的点挤成一团,丧失了原本很重要的特征。
在三维空间也是类似的情况,只有在空间中的点都近似的散布在一个平面上时,投影到这个平面造成的信息丢失最小,分群后的结果与原始的结果也最为近似。PCA算法就提供了一种方式来求取这个需要投影到的空间。
在进行主成分分析之前需要对样本数据进行预处理:
\[x_j^{(i)} = \dfrac{x_j^{(i)} - \mu_j}{s_j}\]然后执行PCA算法,这个算法包含了两部分的内容,一个是求取压缩后的K维空间,还有就是求取样本在K维空间中的投影。
大致的步骤是:
- 计算协方差矩阵(covariance matrix)
- $\Sigma = \dfrac{1}{m}\sum^m_{i=1}(x^{(i)})(x^{(i)})^T$
- 计算协方差矩阵的特征向量
- 在matlab或者octave中可以使用这行代码解决:
[U,S,V] = svd(Sigma);
- 在matlab或者octave中可以使用这行代码解决:
- 取出U矩阵的前k个列并且计算投影后的样本z
整个过程的代码实现是:
Sigma = (1/m) * X' * X; % compute the covariance matrix
[U,S,V] = svd(Sigma); % compute our projected directions
Ureduce = U(:,1:k); % take the first k directions
Z = X * Ureduce; % compute the projected data points
svd()方法实现的效果是奇异值分解
通过Z和U矩阵也可以获得原始数据的一个近似值
选择压缩后的维度
进行维度压缩的时候会造成数据的损失,但是过多的feature又会造成算法运行的缓慢,所以需要选择一个合适的压缩后的维度来压缩数据。通常我们不直接决定压缩后的维度K的值,而是决定我们能允许的数据损失量是多大,数据损失量计算公式为:
\[\dfrac{\dfrac{1}{m}\sum^m_{i=1}||x^{(i)} - x_{approx}^{(i)}||^2}{\dfrac{1}{m}\sum^m_{i=1}||x^{(i)}||^2}\]假如我们能允许的数据损失是1%,就让上面式子的结果小于等于0.01,然后寻找满足这个不等式最小的k的值。
在实际的操作中可以直接使用上面步骤中执行svd()方法的第二个返回值S,S也是一个n * n的矩阵,但是只有对角线上有值,上面那个不等式又可以转化为:
\[\dfrac{\sum_{i=1}^kS_{ii}}{\sum_{i=1}^nS_{ii}} \geq 0.99\]由于S矩阵中记录了$S_{ii}$的值,所以这个方法的计算量不会很大。
运用PCA方法的建议
一般只有在压缩数据或者希望数据可视化时候才考虑使用PCA,正常情况下如果电脑跑的不是很慢尽量还是使用原始数据进行机器学习的方法,PCA方法只运用在训练集的样本中,运用完了之后用得到的映射关系处理验证集和测试集的数据。但是不能使用PCA来处理过拟合的问题,可能进行了PCA处理之后过拟合的问题好像可以消除一点点,但是这个并不是真正的处理了过拟合的问题。还有PCA在整个机器学习的过程中并不是必须的。
参考
所有笔记链接
- [笔记]0.machine-learning-第0篇笔记
- [笔记]1.machine-learning-介绍
- [笔记]2.machine-learning-多元线性回归
- [笔记]3.machine-learning-分类
- [笔记]4.machine-learning-神经网络
- [笔记]5.machine-learning-成本函数和反向传播算法
- [笔记]6.machine-learning-应用机器学习的建议
- [笔记]7.machine-learning-支持向量机
- [笔记]8.machine-learning-分类
- [笔记]9.machine-learning-异常检测
- [笔记]10.machine-learning-大数据量下的梯度下降算法
- [笔记]11.machine-learning-应用示例:照片中的光学字符识别
