[笔记]6.machine-learning-应用机器学习的建议

February 26th, 2017

这一周的内容中主要说的是在机器学习的模型实作完成后，如果发现效果不如预期该从哪一方面着手优化，并提供了一些量化的方法。我们在面对很多问题的时候都是想问题出在哪里，然后往往就是凭感觉认为这里有问题，没有充分的思考就决定在这里开始优化，但是实际上可能费时费力干了几个月发现并没有一点点的效果或者效果并没有那么显著。因此在优化之前一定要好好思考，优化一些更加可能改进的点，这样的优化会更加有说服力，也更加明确自己在做什么，更好的是有时候会更好评估这次优化的效果。

评估假设函数

对于同一个机器学习问题，也许我们能实做出好几个假设函数，但是训练的结果如果仅仅在训练集上进行验证是不合理的。比如现在有100个样本，通过这些样本算出了一个假设函数h1，然后用这个假设函数对这100个样本进行测试，发现这个正确率是100%，然后另外一个假设函数正确率是90%，并不代表正确率高的那个模型就好，因为可能有过拟合的现象，在训练集上表现的好并不代表在实际生产环境中表现好。所以可以在原先的训练集中切出一部分，这部分专门用来进行检测模型对于没有见过的数据的准确率。一般的分法是70%作为训练集（train set），这部分数据喂给模型，帮助模型完善各个参数，剩下的30%是模型训练过程中没有见过的数据(test set)，用来验证模型在生产环境的准确度。

在抽取训练集和测试集的时候需要注意随机抽取，如果数据原本就是随机排列的可以之前取前70%作为训练集，后面30%作为测试集，但是如果数据是以某种顺序排列需要先打乱或者用某些随机算法来分离训练集和测试集。

对于线性回归问题，测试集的误差(The test set error)定义为：

\[J_{test}(\Theta) = \dfrac{1}{2m_{test}} \sum_{i=1}^{m_{test}}(h_\Theta(x_{test}^{(i)}) - y^{(i)}_{test})^2\]

对于分类问题，测试集的误差(The test set error)定义为：

\[err(h_\Theta(x),y) = \begin{matrix} 1 & \mbox{if } h_\Theta(x) \geq 0.5\ and\ y = 0\ or\ h_\Theta(x) < 0.5\ and\ y = 1\newline 0 & \mbox otherwise \end{matrix}\] \[\text{Test Error} = \dfrac{1}{m_{test}} \sum_{i=1}^{m_{test}} err(h_\Theta(x_{test}^{(i)}), y_{test}^{(i)})\]

模型选择和训练/验证/测试集

对于同一种模型，有时候我们会纠结于feature的选取，例如线性回归我们可能会纠结从下面这些模型中挑一种：

\[\begin{cases} h_\theta(x) = \theta_0 + \theta_1 x \newline h_\theta(x) = \theta_0 + \theta_1 x + \theta_2 x^2 \newline h_\theta(x) = \theta_0 + \theta_1 x + \theta_2 x^2 + \theta_3 x^3 \newline ... \newline \end{cases}\]

这时候如果用测试集来评估这些模型的好坏会导致测试集中的样本参与了模型的训练，使最后的准确率不客观，一个替代的方法是引入验证集(Validation Set)的概念，与之前一样，这三个集合的切分应该是随机的，训练集、验证集、测试集的比例分别是60%，20%，20%。

我们现在可以使用以下方法计算三个不同集合的三个单独的误差值：

  1. 使用每个多项式程度的训练集来优化Θ中的参数。
  2. 使用交叉验证集查找具有最小误差的多项式度数d。
  3. 使用具有$J_{test}(\theta(d))$的测试集（d =具有较低误差的多项式的θ）估计误差;

偏差(Bias)和方差(Variance)

偏差和方差都与多项式的维度（feature的最高次项有多少次）有关

在高偏差（欠拟合）的情况下：$J_{train}(\Theta)$和$J_{CV}(\Theta)$都很高。并且这两个值几乎相等

在高方差（过拟合）的情况下：$J_{train}(\Theta)$会变得非常小，但是$J_{CV}(\Theta)$远远大于$J_{train}(\Theta)$，并且随着次数的增大，$J_{CV}(\Theta)$会越来越大

关系可以用下图表示：

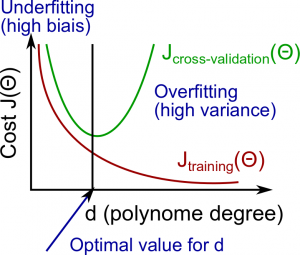
20170226_1

通过对比不同feature的维度下的$J_{train}(\Theta)$和$J_{CV}(\Theta)$可以选取一个合适的维度

正规化和偏差/方差

确定了d的取值之后对于这个模型我们可以进行正规化，来为$\lambda$选取一个合适的值。

可以选取很多的$\lambda$，画出$J_{train}(\Theta)$和$J_{CV}(\Theta)$随着$\lambda$变化的曲线：

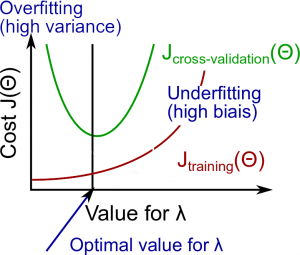
20170226_2

通过曲线可以看出，随着$\lambda$增大$J_{train}(\Theta)$会越来越大（越来越欠拟合），但是$J_{CV}(\Theta)$会减小一段然后增大，原因是一开始减小是模型越来越符合非训练数据，但是增大到一定程度后模型会不适用于所有数据，导致所有的误差都会加大。

通过这个步骤，可以给这个模型选取一个合适的$\lambda$来进行正规化处理

学习曲线(Learning Curves)

学习曲线有助于我们了解随着训练集大小变化，我们的模型表现情况。

在欠拟合的情况下，模型受到训练集的影响不够，当训练集增大时，无论是训练集还是验证集，误差都会很大，展示出来的图形如下所示：

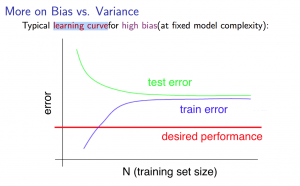
20170226_3

这时候实际的误差和理想的误差会很大，大概高偏差指代欠拟合是从这个图中得到的。这种情况下增加训练集的大小并没有实际的意义，因为误差并不会减小，所以这时候的优化要从其他地方着手。

在过拟合的情况下，模型贴合训练集的样本比较好，但是随着训练集规模的增大，指定的模型没有办法完全贴合训练集中所有的数据，所以训练集规模增大会导致训练集的误差也增大，在另一个方面，不那么可以的贴合训练集样本会导致这个模型更加具有通用性（在没有欠拟合的情况下），所以训练集规模增大会导致验证集误差减小，图形如下所示：

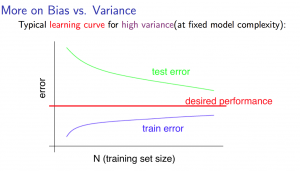
20170226_4

这种情况下增加训练集的大小也许会对最后结果有些帮助。

决定下一步做什么

通常情况下在模型表现不好的时候可以采取下面这些动作，以及对应能实现的效果：

  1. 获取更多的训练集（修正高方差的情况）
  2. 尝试较少的feature（修正高方差的情况）
  3. 增加feature（修正高偏差的情况）
  4. 增加一个feature的维度，比如把x扩展成$x, x^2, x^3, x^4, x^5, x^6… $（修正高偏差的情况）
  5. 减小$\lambda$的值（修正高偏差的情况）
  6. 增加$\lambda$的值（修正高方差的情况）

诊断神经网络

具有较少参数($\Theta$)的神经网络倾向于欠拟合。 它也是计算更便宜。

具有更多参数($\Theta$)的大神经网络易于过拟合。 它也是计算昂贵的。 在这种情况下，您可以使用正则化（增加λ）来解决过拟合。

通常情况是一开始的时候默认只有一个隐藏层。 可以用验证集来尝试不同隐藏层数量的情况。

误差分析

解决机器学习问题的一般步骤是：从一个简单的算法开始，在较短的时间（作者一般在一天）内实现算法，然后查看缺陷。绘制学习曲线，来决定是否需要更多的数据或者更多的feature。然后手动检查验证集上错误的样本，找出错误样本的共同点，着力优化这个部分。

需要用一个单一的指标来评判算法的表现。

偏斜类的误差度量

对于癌症样本的分类，往往得癌症的人数量会非常少，这类样本值为0或者1的样本数量非常不均衡。并且如果仅仅从准确率来判断一个假设模型的好坏是非常不正确的。比如现在有10000个样本，其中有癌症的样本为50个，现在有一个模型预测的正确率达到了2%，如果只看正确率的话，全部预测都直接输出0（没有癌症）的正确率为0.5%，比之前的模型预测还要好一些，然而这个预测是完全没有意义的。所以需要其他的判断标准。

精度（Precision）;

\[Precision = \dfrac{\text{True Positives}}{\text{Total number of predicted positives}} = \dfrac{\text{True Positives}}{\text{True Positives}+\text{False positives}}\]

召回率(Recall):

\[Recall = \dfrac{\text{True Positives}}{\text{Total number of actual positives}}= \dfrac{\text{True Positives}}{\text{True Positives}+\text{False negatives}}\]

准确率(Accuracy)：

\[Accuracy = \frac {true positive + true negative} {total population}\]

精度(Precision)和召回率(Recall)的权衡

精度和召回率的值取决于我们设定的阈值。之前阈值都是设定的0.5，当我们设定阈值为0.7的时候，同一个样本同一个模型的精度会上升，但是召回率会下降。设置一个较低的阈值的时候，召回率会上升但是精度会下降，这时候需要在两者之间权衡。

由于两个变量同时判断很不直观，所以有时候采用F值的方式来判断，这个名称的来历不明，但是可以直接使用这个公式（F值也叫作F1值、F Score）：

\[\text{F Score} = 2\dfrac{PR}{P + R}\]

有时候我们要在验证集上计算F值来判断模型的好坏。

机器学习中的数据

在有些情况下，如果给定够多的数据，有些劣势的算法的效果也能超过其他的算法，一个判断训练集增多能否提升效果的方法是认为观察这些样本，看能不能正确的预测出结果。如果能预测出结果说明这些样本给的信息是足够的，更多的数据往往能解决过度拟合的问题，从而达到更好的效果。但是如果没有人能从样本中看出结果，说明样本中的信息量不够，这时候更多的数据也并不能解决什么问题。

参考

  1. 机器学习 Coursera公开课 by斯坦福大学
  2. Week 6 Lecture Notes

所有笔记链接