- 工具安装
- 多元线性回归(Multivariate Linear Regression)
- 多元线性回归中的梯度下降法
- 梯度下降算法的实践技巧
- 模型的选择
- Normal Equation
- Octave教学
- 参考
- 所有笔记链接
工具安装
这门课使用的工具是Octave或者MATLAB,选择一个就可以了,Octave是免费的工具,matlab也为这门课提供了一个教育版,在三个月的时间内可以使用(2016.11.28 ~ 2017.2.20)。在这门课涉及的知识范围内,两个工具都可以支持。Octave文档:http://www.gnu.org/software/octave/doc/interpreter/
Octave安装说明
windows
我是在这个链接(https://ftp.gnu.org/gnu/octave/windows/)中下载了对应版本的四个文件(不知道有没有全部用到)点击exe直接安装的,需要注意的是不要下载4.0.0的版本,好像是说有个bug,其他新一点旧一点的版本都没问题。
Ubuntu
在terminal中执行这条语句就可以安装成功
sudo apt-get install octave
我安装成功后版本是4.0.0,然而这个版本会导致作业中的代码无法提交的问题,大部分人遇到的问题也许都不一样,建议的方式是换一个版本,可以执行以下指令升级octave
sudo apt-add-repository ppa:octave/stable
sudo apt-get update
sudo apt-get install octave
升级后我电脑中的版本就是4.0.2的了,代码也可以正常提交
多元线性回归(Multivariate Linear Regression)
之前的介绍只考虑了一个feature的情况(假设函数(hypothesis function)只有一个变量x),考虑房子价格时只考虑了面积,但是现实情况是房子的价格不会只与面积有关,往往还会涉及到年限、卧室的数量等等。影响最终结果的因素不止一个的回归分析,叫做多元线性回归。
多元线性回归中的假设函数形式为:
\[h_θ(x)=θ_0+θ_1x_1+θ_2x_2+θ_3x_3+⋯+θ_nx_n\]换成矩阵的写法是:
\[\begin{align*}h_\theta(x) =\begin{bmatrix}\theta_0 \hspace{2em} \theta_1 \hspace{2em} ... \hspace{2em} \theta_n\end{bmatrix}\begin{bmatrix}x_0 \newline x_1 \newline \vdots \newline x_n\end{bmatrix}= \theta^T x\end{align*}\]其中$x_0$假设为1,这样能使两个矩阵的维度相同,方便θ矩阵转置和x矩阵的相乘
然后需要注意的就是一些符号所代表的意思:
$x_j^{(i)} = $ 训练集中第i个元素第j个feature
$x^{(i)} = $ 训练集中第i个元素(所有feature的集合)
m = 训练集中样本的数量
$n = |x^{(i)}|$(feature的数量)
多元线性回归中的梯度下降法
重复以下步骤直到收敛
\[\begin{align*} \lbrace \newline \; & \theta_0 := \theta_0 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_0^{(i)}\newline \; & \theta_1 := \theta_1 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_1^{(i)} \newline \; & \theta_2 := \theta_2 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_2^{(i)} \newline & \cdots \newline \rbrace \end{align*}\]其中$x_0 = 1$,上标表示不同的样本,下标表示feature
可以写成
\[\begin{align*}& \text{repeat until convergence:} \; \lbrace \newline \; & \theta_j := \theta_j - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \; & \text{for j := 0...n}\newline \rbrace\end{align*}\]这种写法其实和之前一元线性回归是一样的,在一元线性回归中:
梯度下降算法的实践技巧
梯度下降法只是从理论上介绍了这个实现的原理,但是还有很多的细节可以加快收敛速度
特征缩放(Feature Scaling)
一种加快收敛的方法是使各个feature的范围大致相同,确保每个feature具有类似的比例,普遍的做法是将范围变成-1到1之间,多一些或者少一些都无所谓
如果不这样统一,有两个feature(不考虑$θ_0$)的时候的轮廓图可以想象一下,会是无数个共用焦点的椭圆,feature之间的范围差距越大,这个椭圆就越瘪,这时候会导致下降速率α很难定义,可能对于一个feature很合适,但是对于另外一个feature就很大,导致不收敛或者收敛很慢。可以这样想象,有一个橄榄球形状的凹面,一个小球沿着边缘某一点往下滑,在一个方向上会来回震荡,而另外一个方向会慢慢的才到最低点。这时候就要把椭球压缩成球体,这时候速率α可以同时满足两个方向。
均值标准化(mean normalization)
其次最好是保持feature的平均值在0附近,这样做的好处可以参照这个链接:http://www.zhaokv.com/2016/01/normalization-and-standardization.html
具体做法就是把feature的数值局限在-1到1这个区间中。实际操作中可以有一定的偏差,没必要完全遵循这个限制。作者给的建议是 [-3, 0.3]、[0.3, 3]都是可以接受的
\[x_i := \dfrac{x_i - \mu_i}{s_i}\]其中μi是feature i的平均值,$s_i$是最大值减去最小值(也可以设置为标准差,在后面的编程作业中是使用的标准差的方法,这边只是为了简单可以设置为范围).
e.g.
feature $x_1$取值在0到3之间,或者$x_2$在-2到0.5之间,这两个就不需要优化了,已经近似的满足这个区间了
如果有feature $x_3$取值在-100到100之间,或者$x_4$在-0.0001到0.0001之间,这种情况就应该优化一下
学习率α的选取
α选取过大可能导致成本函数发散,而选取过小会导致收敛的过程非常缓慢,可以通过画出成本函数$J(θ)$随迭代次数变化的函数来判断α的选取是否合适。
正常的函数图形一般是类似于$\dfrac{1}{x}$的样子:
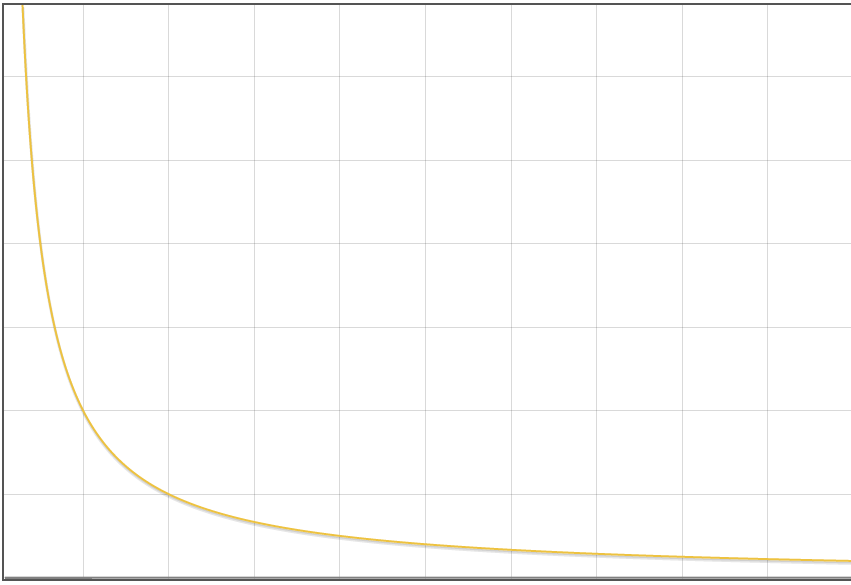
横坐标表示迭代次数,纵坐标表示成本函数的值
成本函数随迭代次数增加下降的越慢(越像$f(x) = 1 - x$)说明α越小,应该增大
成本函数随迭代次数下降反而上升说明α选取过大,应该减小
合适的α基本是不断尝试才得到的,具体可以依次尝试0.001、0.003、0.01、0.03…然后依次观察成本函数随迭代次数变化的图像
不同的问题迭代的次数可能会差别非常大,从几十到几百万都有可能
还有一种判断是否收敛的方法是看一次迭代后成本函数$J(θ)$的减少是否小于某一个值E(一般取$E=10^{-3}$)但是这个用法其实比较不容易判断E到底是否合适
模型的选择
在选择合适的模型的时候需要分析具体的问题而不是直接把已经知道的条件作为feature进行线性拟合
比如知道了房子(假设为长方形)的长和宽,根据经验应该将长和宽相乘作为一个feature来分析,而不是直接构造一个类似于$h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2$的假设函数
再比如通过查看训练数据的分布,发现房子价格随着面积的变化呈现非线性关系,比如说像这样
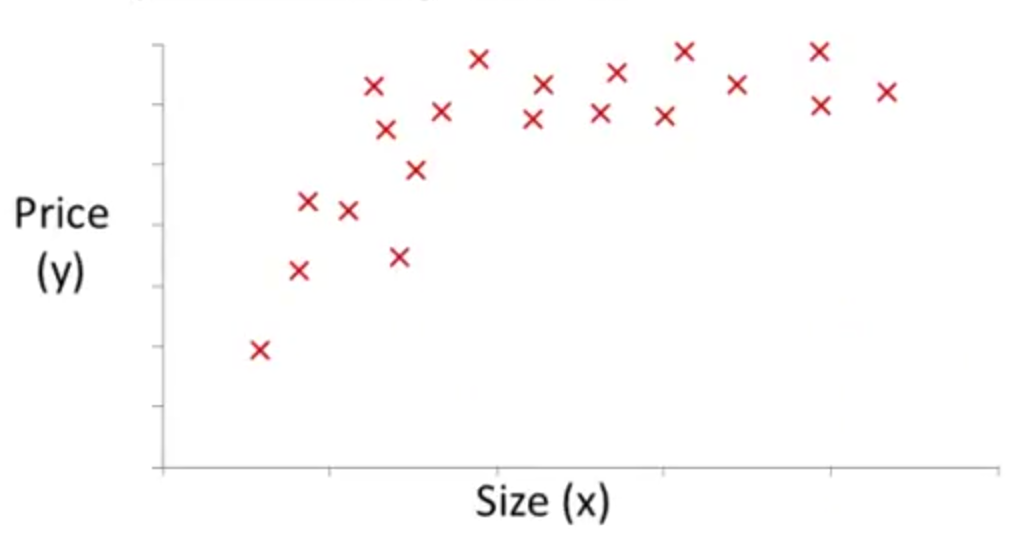
可以考虑将面积和面积的平方作为两个不同的feature来构造模型。这样可以构造出$h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_1^2$
这样的模型,但是按照正常情况是房子的价格不会再面积高到一定程度的时候下降,所以这个模型在面积过大的时候会比较不合理,因此可以考虑这样的情况:$h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_1^2 + \theta_3 x_1^3$。另外一个技巧是直接构造这样的模型:$h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 \sqrt{x_1}$
这种情况需要注意归一化,要不然α很难选
Normal Equation
模型确定之后所需要的步骤就是求解模型的参数,在机器学习中,除了梯度下降算法之外还有一种方法是Normal Equation(找不到对应的中文翻译),首先从求二次方程的极值开始:$J(θ) = aθ^2 + bθ + c$可以通过求J(θ)的导数然后设置导数为0求得θ的值,这时候的θ对应的就是J(θ)的一个极值。类似的,在多维空间中也有相应的定理,想要求取
\[J(\theta_0, \theta_1, ..., \theta_m) = \cfrac{1}{2m} \sum_{i=1}^m( h_\theta(x^{(i)}) - y^{(i)} )^2\]的极值,可以对每个$j \in [0, m]$设置
\[\cfrac{∂}{∂\theta_j}J(\theta_0, \theta_1, ..., \theta_m) = 0\]然后联立这m + 1个方程组可以解出$\theta_0$、$\theta_1$、$\theta_2$、…、$\theta_m$的值,这时候对应的就是J(θ)的极值
实际过程中有另一种简化的方法来获取J(θ)的极值,直接利用公式;
\[\theta = (X^T X)^{-1}X^T y\]课程中没有给公式的推导,实际上看了推导之后发现不难,详细推导可以看这篇博客:https://www.cnblogs.com/elaron/archive/2013/05/20/3088894.html
对于有n个feature,训练集大小为m的情况,X是一个$m * (n+1)$的矩阵(有$x_0$存在),$(X^T X)$和逆矩阵是 (n + 1) * (n + 1)矩阵,乘以$X^T$之后是(n + 1) * m,再乘以y刚好就是(n + 1) * 1的矩阵,也就是(n + 1)维向量。
这个步骤在Octave中很简单,直接输入pinv(X'*X) * X' * y可以解出结果
Normal Equation对比梯度下降法的优势:
- 不需要选取下降速率α
- 不需要经过多次迭代,可以直接得到结果
- 不需要经过标准化的预处理
但是缺点是在n足够大的情况下计算量会非常大,电脑可能承受不住,Normal Equation涉及到多次矩阵的计算,一般n * n的矩阵计算的时间复杂度是$O(n ^ 3)$,所以Normal Equation没办法适用于feature过多的情况。具体来说是差不多以10000为分界线,10000feature之上一般使用梯度下降法,10000feature以下一般使用Normal Equation
在使用Normal Equation的时候可能会遭遇$(X^T X)$是不可逆矩阵(奇异矩阵或退化矩阵)的问题,这个问题出现的概率很低,主要原因可以从下面两个方面考虑;
- 是否存在冗余特征(Redundant features),如果两个特征非常相似或甚至完全相同,就会导致$(X^T X)$是奇异矩阵,比如有两个特征都是关于房屋面积的,只是一个是以平方米为单位,一个以平方英尺为单位,这两个特征并没有什么差别,完全可以从一个特征通过线性变换获取另外一个,所以这个时候做特征的输入量应该删除掉其中的一个特征。不是线性变换得到的这个情况是可以允许的,比如之前构造单个特征的假设方程的时候采取了将面积开根号的方式构造出另一个feature
- feature数量过多(n ≥ m),这时候应该删除一些feature或者使用一种正规化(regularization)的技术(后面的课程中会学到)
由于这个问题很少会出现,Octave的pinv函数做这个运算会得到一个正常的解(但是inv函数不会),所以不需要花太多时间在纠结$(X^T X)$不可逆的问题上
Octave教学
后面部分的内容是Octave常用命令和一些技巧的教学,跟MATLAB比较类似
octave官方文档:http://www.gnu.org/software/octave/doc/interpreter/
或者一般的指令可以直接通过help查看
提交作业是用的一个submit的脚本,在octave的命令行执行submit,然后输入邮箱和随机密码,在win10平台,octave提交作业会遇到一个错误:
!! Submission failed: unexpected error: urlread: Peer certificate cannot be authenticated with given CA certificates
!! Please try again later.
参考
- 机器学习 Coursera公开课 by斯坦福大学
- MATLAB download for Coursera classes
- Index of /gnu/octave/windows
- Octave文档
- 归一化与标准化
- Normal Equations
- Here is the “peer certificate” patch
- Octave for Debian systems
所有笔记链接
- [笔记]0.machine-learning-第0篇笔记
- [笔记]1.machine-learning-介绍
- [笔记]2.machine-learning-多元线性回归
- [笔记]3.machine-learning-分类
- [笔记]4.machine-learning-神经网络
- [笔记]5.machine-learning-成本函数和反向传播算法
- [笔记]6.machine-learning-应用机器学习的建议
- [笔记]7.machine-learning-支持向量机
- [笔记]8.machine-learning-分类
- [笔记]9.machine-learning-异常检测
- [笔记]10.machine-learning-大数据量下的梯度下降算法
- [笔记]11.machine-learning-应用示例:照片中的光学字符识别

