[笔记]5.machine-learning-成本函数和反向传播算法

February 24th, 2017

CostFunction

神经网络的cost function定义为

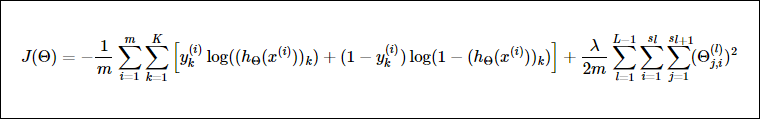
20170224_1

直觉上像是将每个节点的每个输出误差和正规化的惩罚相加

前半部分于逻辑回归的前半部分类似，都是计算预测值和真实值的误差，只是神经网络针对每个输入有多维的输出，所以计算的时候要考虑多维的输出。

后半部分是正规化，防止过度拟合。也是与之前一样对$\Theta$进行累加，同时由于偏置量($a_0^1, a_0^2, a_0^3…$)固定为1，不对这一项的$\Theta$进行惩罚。

反向传播算法(Backpropagation Algorithm)

这个算法用来计算cost function对于每个$\Theta$的偏导数

偏导数和cost function可以用在fminunc这样的函数中直接计算出使$J(\Theta)$最小的$\Theta$

这个算法在课程中没有给严格的证明，只讲了实际操作的步骤。

对于每个输入的样本，执行以下步骤：

  1. 首先计算$a^{(1)}$作为输入
  2. 计算隐藏层和输出层每个节点的值$(a^{(2)}, a^{(3)}… )$
  3. 计算输出层的误差，用预测值减去真实值$\delta^{(L)} = a^{(L)} - y^{(t)}$

  4. 用后一层的误差倒推前一层的误差，计算公式是：$\delta^{(l)} = ((\Theta^{(l)})^T \delta^{(l+1)} .* g(z^{(l)}) .* (1 - g(z^{(l)}))$

    这个地方课程中的公式和课件中都有错误(原文给的公式是$\delta^{(l)} = ((\Theta^{(l)})^T \delta^{(l+1)} .* a^{(l)} .* (1 - a^{(l)})$)，这个公式又是由$g’(z^{(l)}) = a^{(l)}\ .* (1 - a^{(l)})$ 推导得到 主要原因在于g’(z)不等于 $a .*(1-a)$. 应该是 $g’(z) = g(z) .* (1 - g(z))$， 具体可以参考链接2中的 Q2) What is the correct way to compute the sigmoid gradient?

  5. 这里利用公式$\Delta_{i,j}^{(l)} := \Delta^{(l)}_{i,j} + a_j^{(l)} \delta_i^{(l+1)}$(或者向量形式$\Delta^{(l)} := \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^T$)计算每个节点位置的值和误差的乘积，将得到的结果针对每个输入进行累加，得到最终结果我的理解是传输过程中每个路径对所有样本误差的累积。

这个方法的后面两步不太理解，但是按照公式确实是可以得到一个结果，就是做编程练习的时候卡了两天，主要是弄清楚每个变量大概代表的意义，然后弄清楚这些变量的维度会比较容易一些。

最后一步是通过公式计算cost function对于每个$\Theta$的偏微分：

\[D_{i,j}^{(l)} := \dfrac{1}{m}\Delta_{i,j}^{(l)} + \lambda \Theta_{i,j}^{(l)})\] \[D_{i,j}^{(l)} := \dfrac{1}{m}\Delta_{i,j}^{(l)}\]

参数的展开(Unrolling Parameters)

在有多层神经网络的情况下，每一层到下一层都有一个$\Theta$，但是在机器学习习惯性的做法中，是传一个Theta向量给特定的函数，这就需要将每个$\Theta$矩阵中的元素按照顺序排列成一个向量赋值给特定的参数。在处理完之后在分开成为几个$\Theta$。

以一个四层神经网络为例：

$\Theta^{(1)}$（维度10 × 11）

$\Theta^{(2)}$（维度10 × 11）

$\Theta^{(3)}$（维度1 × 11）

展开的方式是 thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]

处理完后可以通过

Theta1 = reshape(thetaVector(1:110),10,11)
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)

得到原先的值，处理的时候要注意Octave中的下标。

梯度检查(Gradient Checking)

经过反向传播算法得到的是$\dfrac{\partial}{\partial\Theta}J(\Theta)$

有另一种方式可以计算这个的近似值：

\[\dfrac{\partial}{\partial\Theta_j}J(\Theta) \approx \dfrac{J(\Theta_1, \dots, \Theta_j + \epsilon, \dots, \Theta_n) - J(\Theta_1, \dots, \Theta_j - \epsilon, \dots, \Theta_n)}{2\epsilon}\]

这个公式在二维平面中很容易理解，好像就是微积分一开始的理论基础，当$\epsilon$足够小，这个表示的就是偏微分。所以我们可以取一个足够小的$\epsilon$来验证结果的正确性，只要两种方法的计算值在每个点上都很相近就表明反向传播算法基本是正确的。

但是一旦验证了这个正确性之后就应该关闭这个检查了，因为这个检查效率很低，非常影响模型跑出来的时间。

随机初始化(Random Initialization)

将所有theta权重初始化为零不适用于神经网络。 当我们反向传播时，所有节点将重复更新为相同的值。

所以在喂给函数初始$\Theta$值之前，应该对$\Theta$进行随机的初始化。

如果想将$\Theta$初始值设定在$[-\epsilon,\epsilon]$之间，可以利用这个方法:

% If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.
% 这里的INIT_EPSILON与参数检查中epsilon的没有任何关系，仅仅是名称相同

Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;

总结

训练一个神经网络模型可以分为以下几步：

  1. 随机初始化权重
  2. 实现每一层的节点的值，最后一层为输出
  3. 实做出cost function
  4. 实现反向传播算法来计算偏导数
  5. 使用梯度检查以确认反向传播能正常，然后禁用梯度检查。
  6. 使用梯度下降或内置优化函数来最小化具有θ的权重的成本函数。

参考

  1. 机器学习 Coursera公开课 by斯坦福大学
  2. FAQ for Week 5 and programming exercise 4

所有笔记链接