[笔记]7.machine-learning-支持向量机

March 2nd, 2017

支持向量机算法（SVM）

SVM是一个监督学习的算法，课程中是一步一步把之前的逻辑回归算法做了一些修改变成了现在的SVM模型。但是SVM只是一种方法，个人感觉课程中的推导过程只是证明了这个方法的合理性，在过滤掉证明过程中的一些奇怪的操作之后，这个方法有着之前所学的逻辑分类所没有的一些特性。

仔细观察没有经过正规化的逻辑回归的cost function：

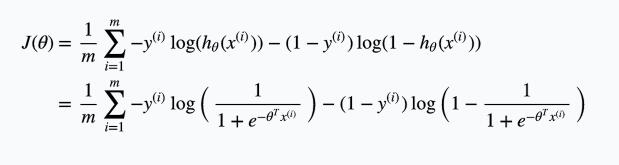
20170302_1

针对其中的

\[-\log(h_{\theta}(x)) = -\log\Big(\dfrac{1}{1 + e^{-\theta^Tx}}\Big)\]

其函数图像为：

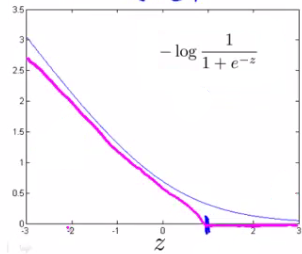
20170302_2

可以对这部分进行一个简化（红色线部分），只有当$z = \theta^Tx > 1$的时候，才认为这个函数输出0，其他时候为一个线性函数: $y = k(1 - z)$

类似的，可以对

\[-\log(1 - h_{\theta(x)}) = -\log\Big(1 - \dfrac{1}{1 + e^{-\theta^Tx}}\Big)\]

进行类似的处理，处理后得到的两个替换的函数标记为$cost_0(z)$和$cost_1(z)$：

\[z = \theta^T x\] \[\text{cost}_0(z) = \max(0, k(1+z))\] \[\text{cost}_1(z) = \max(0, k(1-z))\]

将这两个新定义的函数带到正规化后的逻辑回归cost function后得到：

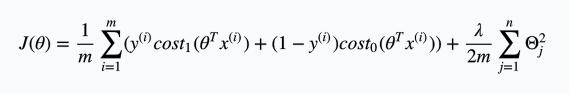
20170302_3

由于针对同一个训练集，训练集的大小m是一个定值，所以直接在cost function中去掉m不会对最终的优化结果产生影响。

所以可以把cost function改写成：

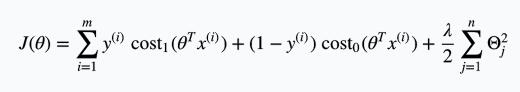
20170302_4

进一步，由于习惯问题，cost function右侧除以$\lambda$，将左侧的系数写成C，得到：

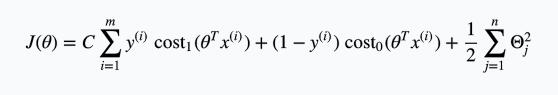
20170302_5

SVM方法需要做的内容就是最小化这个cost function

C的作用和$\lambda$的作用相同，都是为了防止过拟合，但是之前是$\lambda$值增大防止过拟合，现在是C值减小防止过拟合。

最后需要注意的是SVM的$h_\theta(x)$输出值只有0和1，而不是像逻辑回归一样输出一个几率值。

Large Margin Intuition

SVM被称为一个大边界分类器(large margin classifiers)，主要是因为上面图中cost function的设定：

  • 如果希望y = 1，需要$\Theta^T x \ge 1$ 而不仅仅是大于0
  • 如果希望y = 0，需要$\Theta^T x \le -1$而不仅仅是小于0

如果现在出现C特别大的情况，为了最小化cost function，我们需要想办法将

\[y^{(i)} cost_1(\theta^Tx^{(i)}) + (1 - y^{(i)}) cost_0(\theta^Tx^{(i)})\]

尽量接近0。

这样一来cost function的值只与$\dfrac{1}{2} \sum_{j=1}^n \Theta_j^2$有关，这将会导致决策边界出现下图中黑色线的样子

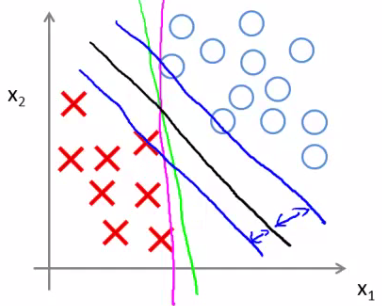
20170302_6

这条线会尽量与正负样本保持足够大的距离

证明过程在Mathematics Behind Large Margin Classification (Optional)这部分，是用向量X乘来证明的，不过视频上好像没太说清楚，应该直觉上还比较好理解。

但是如果一群负样本中掺杂了一个正样本，就会导致决策边界很诡异，这也就是过度拟合的现象，解决办法是降低C的大小避免过拟合。

Kernels: SVM用于非线性分类器

前面提到的SVM只能用在线性分类中，但是SVM提供了一种kernel的技术，能使SVM成为一个非线性的分类器。

一个应用kernel的做法是替换之前的feature，使用$f_1, f_2, f_3, …$来替换$x_1, x_2, x_3, …$， 其中$f_i$的定义为：

\[f_i = similarity(x, l^{(i)}) = k(x, l^{(i)}) = \exp(-\dfrac{||x - l^{(i)}||^2}{2\sigma^2})\]

这里用到的kernel就是similarity函数，也被成为是高斯内核(Gaussian Kernel)，这个函数描述了每个样本相对所有样本的距离，函数中的$l^{(i)}$就代指所有的样本。

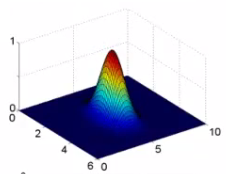
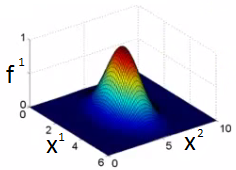
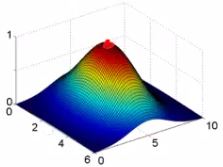
这里的$\sigma$指的是标准差，定义了地标上升的陡峭度，有点像是允许的误差大小，当$\sigma$越小的时候，整个similarity函数就越陡峭，反之就越平缓，但是峰值都是1，这里可以联想到平面中的正态分布，这里的$\sigma$与正态分布中的$\sigma$应该是一样的。

可以通过不同取值观察函数图形直观的看出$\sigma$的作用，下面三幅图中$\sigma$取值分别是0.5，1，3：
20170302_7
20170302_8
20170302_9

当$x \approx l^{(i)}$的时候，$f_i = \exp(-\dfrac{\approx 0^2}{2\sigma^2}) \approx 1$

当x离$l^{(i)}$很远的时候，$f_i = \exp(-\dfrac{(large\ number)^2}{2\sigma^2}) \approx 0$

将这个kernel用在SVM上，得到SVM的优化目标是：

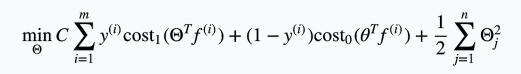
20170302_10

需要注意的是这里f的维度和之前x的维度是不一样的：

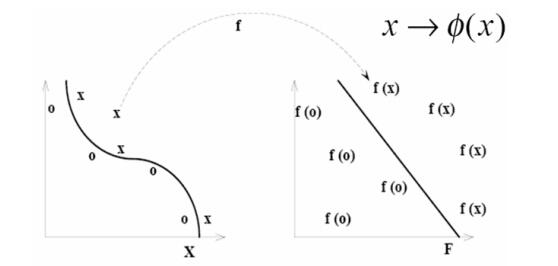
\[x^{(i)} \rightarrow \begin{bmatrix}f_1^{(i)} = similarity(x^{(i)}, l^{(1)}) \newline f_2^{(i)} = similarity(x^{(i)}, l^{(2)}) \newline\vdots \newline f_m^{(i)} = similarity(x^{(i)}, l^{(m)}) \newline\end{bmatrix}\]

有点像是将维度向上升了一级，就是将x映射到了更高维的特征空间(feature space)中去了，然后在高维度中使用线性分类器处理样本

20170302_11

使用SVM

目前SVM方法已经有很多人都在使用了，大部分机器学习的library中也已经用很好的方法实现了SVM，我们仅仅需要用合适的参数调用API就可以了。

使用SVM需要注意的事情：

  1. 选取合适的参数C
    • 过拟合的话减小C的值
    • 欠拟合的话增大C的值
  2. 选取kernel
    • 这个课程中只介绍了similarity function
    • 如果不选取kernel的话就会直接使用线性分类器
  3. 如果选取了高斯kernel，还需要选取方差($\sigma^2$)大小

逻辑回归(Logistic Regression) vs. SVMs

  • 如果n相对于m很大，则使用逻辑回归或者没有kernel的SVM
  • 如果n比较小，m没有很大，则使用高斯kernel的SVM方法
  • 如果n很小，m很大，则需要添加或者构造更多的feature，然后使用逻辑回归或者没有kernel的SVM

神经网络可能适用于这三种情况，但是训练得会比较慢

参考

  1. 机器学习 Coursera公开课 by斯坦福大学
  2. Week 7 Lecture Notes
  3. Support Vector Machines 簡介 林宗勳 (daniel@cmlab.csie.ntu.edu.tw)
  4. 支持向量机通俗导论（理解SVM的三层境界） - 结构之法 算法之道
  5. 12: Support Vector Machines (SVMs)

所有笔记链接