Playing flappy bird with Deep Reinforcement Learning
理论部分基于DeepMind的paper: Playing Atari with Deep Reinforcement Learning
主要是参考下面两个之前已经有了的实现,网络的架构完全没有更改,只是当做练习重新做了一遍
文章地址: https://junmo1215.github.io/machine-learning/2017/06/26/Practice-Playing-flappy-bird-with-DRL.html
代码地址: https://github.com/junmo1215/rl_games/tree/master/flappy_bird
代码架构
flappy_bird
-- assets/
-- game/
-- images/
-- main.py
-- rl_brain.py
其中assets、game、images这三个文件夹都是直接从之前的实现中复制过来的,是游戏的引擎部分,只适配Python3改了一点点内容,不是算法的核心部分
剩下的两个文件是比较关键的部分,要理解这两个文件的内容,需要了解一下Deep Reinforcement Learning的算法细节:

算法说明
1. 初始化部分
初始化神经网络和Memory List(作用在后面讲)
2. 外层for循环(for episode = 1, M):
每一次循环代表一次游戏过程,放在这个例子中就是从游戏开始画面上出现小鸟到小鸟撞到水管或者地面,通过一次次不断的尝试不断修正神经网络中的参数,为了让网络更加准确。
3. 内层for循环(for t = 1, T):
这里的每个循环代表着游戏的每一步,可以大致的理解成画面的每一帧,在每次循环中需要先选取一个动作(按下屏幕让小鸟跳跃或者什么都不做),然后游戏引擎收到这个动作之后会返回新的游戏画面和reward以及告诉玩家游戏是否结束。于是我们就可以不断的获得 {state_1, action_1, reward_1, state_2, action_2, …, state_n, action_n, reward_n, state_T} 这样的一个集合。剩下的就是需要从很多这样的集合中学到这个游戏应该怎么玩(这个集合在实际的算法实现中有一些改变,这里只说大致的逻辑)
核心的学习部分基于两个假设:
- MDP(Markov Decision Process)马尔科夫决策过程:下一个状态仅仅取决于当前的状态和当前的动作。当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态;换句话说,在给定现在状态时,它与过去状态(即该过程的历史路径)是条件独立的,那么此随机过程即具有马尔可夫性质。具有马尔可夫性质的过程通常称之为马尔可夫过程。https://zh.wikipedia.org/wiki/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E6%80%A7%E8%B4%A8
- bellman equation:在一个序列求解的过程中,如果一个解的路径是最优路径,那么其中的每个片段都是当前的最佳路径(这个还比较好理解,具体可以参照演算法相关资料)。在这里可以理解成,从起点到终点会经过很多状态(假设$s_1$, $s_2$, $s_3$, … ,$s_t$)。假设这条路径是整体reward最大的路径,那么其中的一些片段,比如{$s_1$, $s_2$, $s_3$} 就是 $s_1$ 到 $s_3$ reward最大的路径。
从这两个假设中可以得到一些推论,这里直接给出结果:
我们可以对每个状态的每个动作进行一个估值(这个估值表示的意思是这个状态的好坏),在每个状态中,选取估值较大的那个动作,这样我们就能到达下一个状态了,在下一个状态中采取相同的动作,以此类推我们可以最终到达终点。由于每一步都是力图达到最终结果最优的策略,因此如果这个估值足够准确的话,我们在游戏中执行的每一步就是当前的最优步骤,并且最终结果也是最优的。
所以我们的目标就是要获取每个状态下每个动作的估值。这篇paper的实作方式是用一个神经网络来估计这个状态的价值,目标是让这个神经网络给出的估值尽可能准确。
神经网络架构
神经网络的架构图(按照之前的实作yenchenlin/DeepLearningFlappyBird: Flappy Bird hack using Deep Reinforcement Learning (Deep Q-learning)):
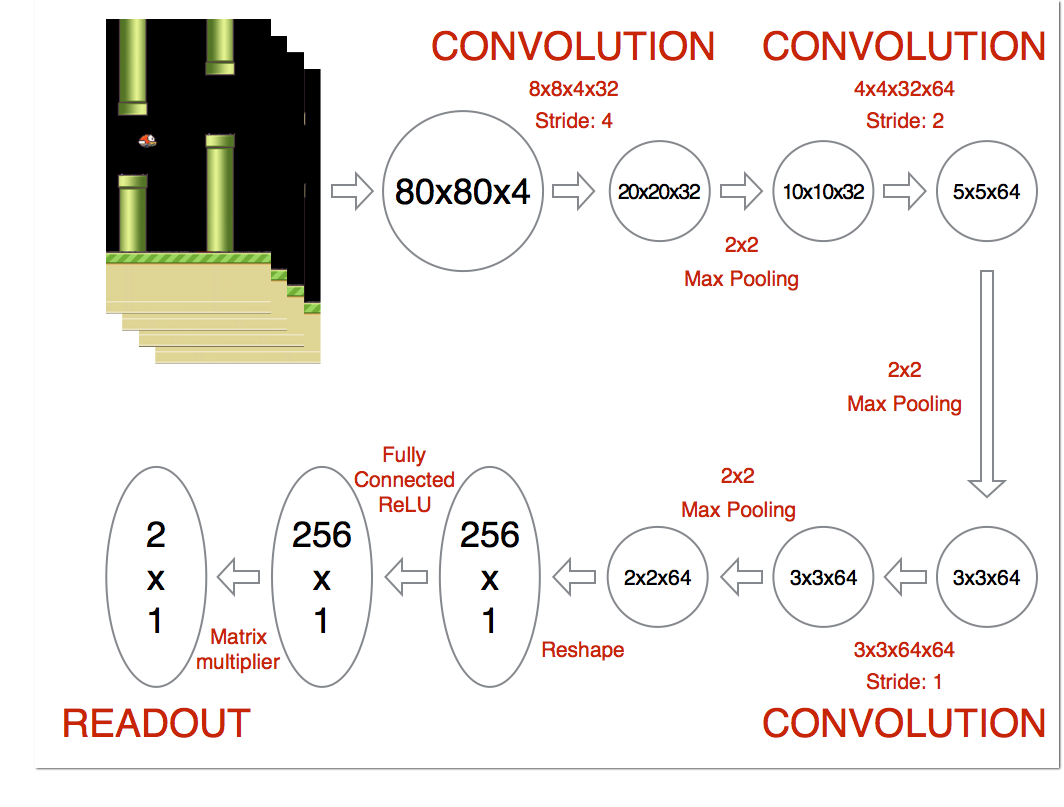
网络架构是拿到游戏状态(每个样本维度是 80 * 80 * 4),然后卷积(输出维度 20 * 20 * 32)、池化(输出 10 * 10 * 32)、卷积(输出 5 * 5 * 64)、卷积(输出 5 * 5 * 64)、reshape(1600)、全连接层(512)、输出层(2)
具体的实现和上图中有一些差别(主要是第二次和第三次卷积之后少了池化的操作,然后全连接层的维度改了),具体原因不清楚,目前我对于网络的设计和参数的调节都还不太熟练
实作细节
- 游戏引擎给出的游戏画面大小是(512 * 288),第一步是把引擎给出的图像变成黑白并且缩放成(80 * 80)。因为需要用到卷积,所以图像的长宽需要相同
- 然后不是用单个图像画面来表示一个状态,而是使用四个连续画面来表示当前的状态,所以每个状态的维度就是(80 * 80 * 4) 这个做法还不太清楚必要性,可能是增加状态的辨识度?
- 拿到单个状态之后,喂给神经网络,输出两个action分别的价值。
- 选择action的时候不是每次都选择估值最大的那个,而是有一个概率值,按照一定的概率选择估值最大的action,其他时候随机选择action。这样做的目的是为了避免有的状态永远遍历不到,让AI尽可能尝试多的状态。这个概率初始的时候是在0.1(INITIAL_EPSILON)左右的一个比较小的值,随着训练次数的不断增加,让这个值越来越小,这样处理可以让神经网络在成熟了之后不去轻易尝试其他的action。举个例子:假如现在这个小鸟已经飞的很好了,如果还是一直保持着10%随机动作的概率,有可能在过一个水管不该起跳的时候跳了一下导致重头再来。虽然这样会多一次失败的教训,但是会让小鸟在之前已经很熟练的地方尝试很久,让熟练的地方更加熟练。(在这个游戏中没有很明显,但是其他游戏中这个做法我个人感觉还是比较有必要的,这个游戏因为重复率太高了所以其实没什么关系)
代码的架构参照莫烦Python里面的写法,感觉这系列的视频挺好入门的
main.py
def main():
begin_time = datetime.datetime.now()
# 首先初始化游戏引擎和神经网络
env = game.GameState()
brain = DeepQNetwork(
n_actions=N_ACTIONS,
memory_size=MEMORY_SIZE,
minibatch_size=MINIBATCH_SIZE,
gamma=GAMMA,
epsilon=INITIAL_EPSILON
)
step = 0
for episode in range(MAX_EPISODE):
# do nothing
# 每次游戏过程中,在游戏开始的时候输入一个什么都不做的动作,让引擎给出一个初始游戏画面,并且用这个画面初始化神经网络的第一个状态
observation, _, _ = env.frame_step([1, 0])
observation = preprocess(observation, False)
brain.reset(observation)
while True:
# 当前游戏画面选择合适的动作。选取的action并不是每次都选取估值最高的那个,而是有一定的概率随机选择(参照细节4)
action = brain.choose_action(observation)
# 有了当前应该采取的动作之后就把这个动作喂给游戏引擎,引擎返回下一个游戏画面,这个动作的reward和游戏是否结束的标识
observation_, reward, done = env.frame_step(action)
observation_ = preprocess(observation_, True)
# 将这一步的相关信息存到大脑中,方便之后取出来学习
brain.store_transition(observation, action, reward, done, observation_)
# 有一定的记忆就可以开始学习了
if step > 200:
brain.learn()
if done:
break
# 更新相关的标识
observation = observation_
step += 1
end_time = datetime.datetime.now()
print("episode {} over. exec time:{} step:{}".format(episode, end_time - begin_time, step))
env.exit("game over")
这个文件中之前实作的作者的写法是用一个大的循环来进行的,其实这样做也是可以。因为主要是把每次 {observation, action, reward, done, observation_} 的信息存到记忆中,这个游戏引擎在游戏结束的时候会返回一个初始的游戏画面(没记错好像是这样)。造成的差别只有在每次挂掉重新开始时候的那三帧画面对应的state有点不一样,以第一帧为例,之前的实现是{$s_{t-2}$, $s_{t-1}$, $s_t$, $s_0$}(其中t是挂掉的时间点),我的实现中是{$s_0$, $s_0$, $s_0$, $s_0$},其实感觉对于这里来说没什么影响。我这么写只是个人喜好,虽然代码里面多了一个循环,但是感觉表达的意思直观一些。
rl_brain.py
可以把这个文件想象成是大脑,里面有一些记忆(memory_list),记忆的空间有个大小(memory_size),有一个神经网络能把输入的状态转换成当前状态下每个动作的估值(_create_network),并且能将当前游戏画面(结合之前的三帧画面)整合成一个状态,根据上面这两个功能,可以根据当前游戏画面选择一个合适的action(choose_action)。然后体现这个大脑学习能力的就是learn这个方法了,这个方法中能从记忆中抽取小批量的数据来不停的修正神经网路的权值,让神经网络更加准确。
下面对一些主要的方法进行说明:
def __init__(
self,
n_actions,
memory_size,
minibatch_size,
gamma,
epsilon
):
self.n_actions = n_actions
self.memory_size = memory_size
self.memory_list = []
self.minibatch_size = minibatch_size
self.time_step = 0
self.gamma = gamma
self.epsilon = epsilon
self.current_state = None
self._create_network()
初始化函数,相关的参数在后面具体用到的时候会有说明
def reset(self, observation):
self.current_state = np.stack((observation, observation, observation, observation), axis=2)
每次挂掉之后调用这个函数,用初始画面整合出初始的状态,没有这个函数也是可以,就像原始作者的那个做法一样,用挂掉之前的画面跟初始画面结合来填充。我个人比较喜欢这样的写法,直观一些,并且不需要单独处理游戏第一次打开的时候连之前挂掉的画面都没有的情况。
current_state这个变量中记录最近四帧游戏画面,整合成一个state。具体用四帧画面表示一个state做法的说明见实作细节当中的第二点
def store_transition(self, observation, action, reward, done, observation_):
"储存要训练的内容"
next_state = np.append(observation_, self.current_state[:, :, :3], axis=2)
self.memory_list.append([self.current_state, action, reward, done, next_state])
if len(self.memory_list) > self.memory_size:
del self.memory_list[0]
self.time_step += 1
记录当前游戏画面,选择的动作等信息,方便之后拿出来训练。
同样要注意的是存储的不是游戏画面而是state(最近的四帧画面)
这里还要注意一下memory_list中存的顺序,后面要按照这个索引取出相应的值
def choose_action(self):
"根据当前状态选择要执行的动作"
n_actions = self.n_actions
action = np.zeros(n_actions)
if random.random() <= self.epsilon:
action_index = random.randrange(n_actions)
action[action_index] = 1
else:
# 只输入了一个状态
q_value = self.q_value.eval(feed_dict={self.state_input: [self.current_state]})[0]
action_index = np.argmax(q_value)
action[action_index] = 1
if self.epsilon > 0.0001:
self.epsilon -= (0.1 - 0.0001) / 3000000
return action
根据当前游戏画面选择动作,由于将current_state储存起来了,所以这边不需要传参数。
epsilon是一个概率的阈值,如果随机的结果大于这个值就按照估值最高的方式走,否则执行一个随机的动作。并且这个阈值会随着时间的推移慢慢降低,越来越少的去尝试随机动作。具体原因参照实作细节第四点
def learn(self):
"训练步骤"
minibatch = random.sample(self.memory_list, self.minibatch_size)
# 索引要和前面store_transition中的顺序一样
state_batch = [data[0] for data in minibatch]
action_batch = [data[1] for data in minibatch]
reward_batch = [data[2] for data in minibatch]
# 第三列记录的内容是是否终止
next_state_batch = [data[4] for data in minibatch]
act_q_value_batch = []
next_q_value_batch = self.q_value.eval(feed_dict={self.state_input: next_state_batch})
for i in range(self.minibatch_size):
act_q_value = reward_batch[i]
# 下一个状态没有终止的话还需要加上之后状态的衰减
if not minibatch[i][3]:
act_q_value += self.gamma * np.max(next_q_value_batch[i])
act_q_value_batch.append(act_q_value)
self.train_step.run(feed_dict={
self.action_input: action_batch,
self.state_input: state_batch,
self.act_q_value: act_q_value_batch
})
# save network every 100000 iteration
if self.time_step % 10000 == 0:
self.saver.save(self.session, 'saved_networks/network-dqn', global_step=self.time_step)
def _create_network(self):
# network weights
w_conv1 = self._weight_variable([8, 8, 4, 32])
b_conv1 = self._bias_variable([32])
w_conv2 = self._weight_variable([4, 4, 32, 64])
b_conv2 = self._bias_variable([64])
w_conv3 = self._weight_variable([3, 3, 64, 64])
b_conv3 = self._bias_variable([64])
w_fc1 = self._weight_variable([1600, 512])
b_fc1 = self._bias_variable([512])
w_fc2 = self._weight_variable([512, self.n_actions])
b_fc2 = self._bias_variable([self.n_actions])
# input layer
# 当前状态
self.state_input = tf.placeholder("float", [None, 80, 80, 4])
# hidden layers
h_conv1 = tf.nn.relu(self._conv2d(self.state_input, w_conv1, 4) + b_conv1)
h_pool1 = self._max_pool_2x2(h_conv1)
h_conv2 = tf.nn.relu(self._conv2d(h_pool1, w_conv2, 2) + b_conv2)
h_conv3 = tf.nn.relu(self._conv2d(h_conv2, w_conv3, 1) + b_conv3)
h_conv3_flat = tf.reshape(h_conv3, [-1, 1600])
h_fc1 = tf.nn.relu(tf.matmul(h_conv3_flat, w_fc1) + b_fc1)
# Q Value layer
self.q_value = tf.matmul(h_fc1, w_fc2) + b_fc2
# 当前状态选择的action
self.action_input = tf.placeholder("float", [None, self.n_actions])
# 当前状态实际的q_value
self.act_q_value = tf.placeholder("float", [None])
# 按照经验预测出的q_value(Q(s_t, a_t))
pred_q_value = tf.reduce_sum(tf.multiply(self.q_value, self.action_input),
axis=1)
self.cost = tf.reduce_mean(tf.square(self.act_q_value - pred_q_value))
self.train_step = tf.train.AdamOptimizer(1e-6).minimize(self.cost)
# saving and loading networks
self.saver = tf.train.Saver()
self.session = tf.InteractiveSession()
self.session.run(tf.initialize_all_variables())
checkpoint = tf.train.get_checkpoint_state("saved_networks")
if checkpoint and checkpoint.model_checkpoint_path:
self.saver.restore(self.session, checkpoint.model_checkpoint_path)
print("Successfully loaded:", checkpoint.model_checkpoint_path)
else:
print("Could not find old network weights")
应该是这个文件里面最核心的一块地方了,之前我在这里卡了很久,主要是之前没有弄清楚算法的精华。要弄清楚这里面的细节,需要明白这个算法是依据什么来进行优化的。之前的篇幅中也一直在回避这个问题。这里大概的解释一下(在这部分忽略游戏画面(observation)和状态(state)的区别,所有用词都表示一个状态,为了理解的直观,也可以把一个游戏画面就想象成是一个状态):
前面算法说明部分提到过,这个网络的目标是尽可能准确的获取每个状态下每个动作的估值。需要分辨清楚的是这里的估值指的是游戏按照目前策略进行下去最终的得分而不是这个动作反馈的值,后者是游戏引擎返回的reward(这个动作产生的得分)。把状态记做s,选择的动作是a,这个估值记做Q,我们的目标就是得到一个(s, a)到Q的映射关系。这个关系就是神经网络。
接着需要理解的一个地方就是下面这个公式:
\[R_t = \sum^T_{t'=t} \gamma^{t'-t} r_{t'}\]其中$r_t$表示t时刻的reward,T表示终止的时刻,$\gamma$是一个衰减的系数
这个公式我目前都没有非常清楚的理解,只能说说我目前的感觉,$R_t$指的是当前这个状态的好坏(非常感谢这篇文章的这个理解 Deep Reinforcement Learning 基础知识(DQN方面) - songrotek的专栏 - 博客频道 - CSDN.NET 感觉比以前稍微懂了一些),这个好坏不仅仅取决于目前直观返回的reward,还取决于未来状态的这个指标(如果当前的reward比较高,但是接着来的下一个状态很差也会拉低当前状态的这个值)。但是未来状态的这个指标对目前的影响是有限的,离目前状态越远的状态对当前状态的这个指标的影响就越小,所以后面的状态会带有一个衰减系数的(t’ - t)次方。
现在需要做的是把这个公式和神经网络结合起来。前面提到过,神经网络的输入是(s, a),输出是Q,表示当前状态下这个动作的估值,仔细想想,这个估值就是公式里面提到的$R_t$。估值越高表示这个状态越好。
这里神经网络的输入输出有点不严谨,但是看下代码应该是可以理解这部分,其实输入是s,输出是每个action对应的Q
现在的思路就是假设我们已经有了一个神经网络,不管这个网络表现的好不好先用着,只要能有办法慢慢的修正网络中的参数让网络表现的越来越接近理想的结果就行了。所以我们要考虑一个方法让网络能往正确的参数靠弄。
一个想法是用两个方法表示同一个值,如果说网络表现绝对理想,这两个值应该是一样的,在不理想的情况下,就能用两种方式计算的结果的误差大小衡量网络的好坏,尽可能通过训练数据让这个值缩小,我们就能得到一个性能相对较好的网络。重复很多次之后这个网络的表现就会越来越好。其实这个值已经在之前有提到过了:就是当前的估值$R_t$
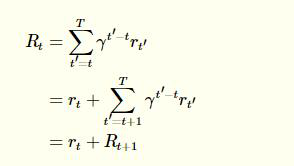
由于我们很容易获取到t和t+1时刻的状态,只需要把这两个时刻的状态转换成$R_t$和$R_{t+1}$就行了(需要注意的是如果t时刻就是终止状态就没有t+1时刻,这时$R_t = r_t$)
所以在learn这个函数里面的逻辑是:
- 拿到当前状态s和当前动作a,喂给神经网络能获取这个情况下的Q(代码里面是pred_q_value)
- 用下一个状态s’,喂给神经网络,由于动作没有确定,所以选择估值最高的一个动作得到act_q_value
- 定义 $ \text{cost_function} = (\text{pred_q_value} - \text{act_q_value})^2 $
- 用Adam算法训练神经网络使cost_function最小(这一步tensorflow已经封装好了直接用就行tf.train.AdamOptimizer(1e-6).minimize(self.cost))
其他的事情就是喂数据给这个网络让网络不停的优化就可以了。
运行
运行所需环境
- Python2.7 or Python3.5以上
- TensorFlow 1.0 以上
- windows系统tensorflow GPU版本目前只支持python 3.5
- windows tensorflow安装教程
- Ubuntu tensorflow安装教程
- pygame
- openCV-Python
运行
- 查看效果:
python main.py
- 继续训练(如果要重新训练删除saved_networks里面的文件就行了)
python main.py train
不足
- 虽然会隔一段时间保存一次神经网络的参数,但是 INITIAL_EPSILON 和 memory_list 没有保存下来,每次重新训练又会初始化一次,但是应该没有太大的影响
- _create_network里面的代码包含了costfunction,分开的话看的清楚一些
参考
- Playing Atari with Deep Reinforcement Learning
- yenchenlin/DeepLearningFlappyBird: Flappy Bird hack using Deep Reinforcement Learning (Deep Q-learning)
- 用Tensorflow基于Deep Q Learning DQN 玩Flappy Bird - songrotek的专栏 - 博客频道 - CSDN.NET
- Paper Reading 1 - Playing Atari with Deep Reinforcement Learning - songrotek的专栏 - 博客频道 - CSDN.NET
- Deep Reinforcement Learning 基础知识(DQN方面) - songrotek的专栏 - 博客频道 - CSDN.NET
- 莫烦Python
- 马尔可夫性质 - 维基百科,自由的百科全书
