[实作]TDLearning in 2584-fibonacci (二)、实现TD0

November 27th, 2017

2584-fibonacci game

涉及的知识点目前有：

  • 2584的基本规则
  • C++基本语法
  • Temporal Difference Learning
  • N-Tuple Networks

文章地址： https://junmo1215.github.io/machine-learning/2017/11/27/practice-TDLearning-in-2584-fibonacci-2nd.html

代码地址： https://github.com/junmo1215/rl_games/tree/master/2584_C%2B%2B

由于后面几个project持续在做，所以获取的代码应该是后面几个project版本的代码，可以根据签入记录获取对应的版本。代码也许有略微差异，但是应该不影响理解。

基础知识

TD(0) / Qlearning

这里开始我们要实作2584的AI了，让AI自己学着玩这个游戏。参考这篇paper 的思路，这个实作里面用的是TD(0)，也就是Qlearning，这里面不详细证明Qlearning的迭代规则，只是简单讲讲大致的思路。

首先我们要把游戏过程想象成一个个的状态（state，或者是想象成游戏画面），对于某一个状态，我们能做出相应的动作(action，什么都不做也可以考虑成一个什么都不做的action，虽然2584中没有这个情况)，然后游戏会产生一个变化，这个变化包含目前有没有得分(reward)，以及游戏画面(state)会产生一些变化。所以游戏流程可以看成有很多的state，我们分别记做: $ s_1, s_2, …, s_T $ ，（$s_T$是最终的游戏状态）。考虑一个让最终得分最高的策略，在t时刻，我们要做出相应的动作 $ a_t $ 。所以现在变成了这个动作该怎么选择的问题，Qlearning的方式是对于每个state，我们列出一张表格，这个表格中记录了每个状态对应每个动作的期望值，这个值越高说明这个状态下选择这个动作越好。现在选择动作就很简单了，对于每个状态我们就去这个表里面查所有动作的值（Q value），直接选择值最大的这个动作。

上面的这个选择动作的策略可行的一个前提条件是我们需要有这么一张表，这个表格不会凭空产生，里面的值需要我们想办法得到，具体得到的方法可以结合我们自己的学习流程。我们假象这样一个例子：在放学回家后，你没有写作业而直接开始玩游戏了，家长看到后教训了你一顿；第二天放学回家，直接就去写作业了，家长回来表扬了你；那么第三天放学回家没有写作业的时候你应该知道要怎么做了。把这个假象实验提取一下关键信息就是，对于一个state（放学回家没有写作业），如果我们选择的一个动作action（第一天的玩游戏）产生了不好的影响reward（被家长教训），那么之后我们就会少选择这个动作（减少表格中这个状态下对应这个动作的值）；如果我们选择了一个动作（第二天的写作业）产生了一个好的影响（被家长表扬），那么之后我们在这个状态下就应该多选择这样的动作（增加表格中这个状态下对应这个动作的值）。

目前还需要考虑的问题是有时候长时间没有反馈，我们怎么知道这个时候选择的这个动作是好还是坏呢，比如你放学回家开始玩游戏，家长没有说你，但是你玩了两小时游戏后开始看电视然后吃零食，吃饭挑食什么的，接着你家长就大发雷霆了，你就需要反思是哪个环节的选择不太对，怎么知道放学回家不该直接玩游戏呢。我们可以继续使用这个paper的思路，在2584的游戏中，我们每个状态都可以尝试一下上下左右这四个动作（要排除划不动的情况），然后会分别产生四个不同的盘面以及这一步的得分。我们针对下面这个局面来进行说明：

原始盘面：
+------------------------+
|     1     0     0     0|
|     0     0     0     0|
|     1     8     0     0|
|     2     3     8     3|
+------------------------+

slide left      reward: 5
+------------------------+
|     1     0     0     0|
|     0     0     0     0|
|     1     8     0     0|
|     5     8     3     0|
+------------------------+

slide down      reward: 3
+------------------------+
|     0     0     0     0|
|     0     0     0     0|
|     1     8     0     0|
|     3     3     8     3|
+------------------------+

slide right     reward: 5
+------------------------+
|     0     0     0     1|
|     0     0     0     0|
|     0     0     1     8|
|     0     5     8     3|
+------------------------+

slide up        reward: 2
+------------------------+
|     2     8     8     3|
|     2     3     0     0|
|     0     0     0     0|
|     0     0     0     0|
+------------------------+

这里列出了上下左右滑动给出的得分和接下来的盘面，得分我们可以看得到，但是怎么知道接下来盘面的好坏呢。这时候就该想到我们正在迭代的这个表格了，我们的表格中同样会有下一个状态对应的信息，对应四个动作的估值。通过这个我们就能知道，在下一个状态选的再好，评分也不会比这四个动作的最高值高，所以我们会把下一个状态中四个动作的最高值代表这个状态的估值。简单来说就是用下一个状态的估计的值和当前动作得到的reward来评价目前这个状态的好坏。

在实作的时候有一个细节跟这里讲的不一样，如果只按照这个实作的话有些不严谨，结果似乎也不会太好。这里只是介绍大概的原理和思路。

在这个实作中，我们就是基于这个策略一步步的迭代我们的表格，让每个状态对应的值越来越准确。这一步看上去有点玄学，用一个不准确的东西跑很多次怎么就会有一个准确的结果，还是这篇paper给出了详细的证明，他们推导了Qlearning的理论基础，并且通过实验证明了这种方式是有效的。我们这次的实作也可以看作是这个paper的实验，最终也能发现确实这个方法是可行的。其实就是一次次的迭代让计算出的结果越来越准确。

N-tuple

跟2048不同的是，2584的最大可能性是第32个数，也就是每个格子都有32中可能，这样一来状态一共有 $32^{16}$ 种，建立的Q表会特别大以至于存不下去，因此根据这篇paper：Temporal difference learning of N-tuple networks for the game 2048 ，有人提出用盘面中的一些特征(feature)来代表当前状态，我们不直接在表中查出当前盘面多少分，而是查出每个特征多少分，再把这些特征加起来代表整个盘面的分数。在这个实作中特征的选择方法是根据盘面特定位置的方块来的，我们可以用一个一维数组表示盘面：

 index (1-d form):
  (0)  (1)  (2)  (3)
  (4)  (5)  (6)  (7)
  (8)  (9) (10) (11)
 (12) (13) (14) (15)

然后feature就是特定位置的值组合起来，比如下面这个盘面：

+------------------------+
|     1     0     0     0|
|     0     0     0     0|
|     1     8     0     0|
|     2     3     8     3|
+------------------------+

一个feature是{ 0, 4, 8, 9, 12, 13}。
（这里的0， 4， 8... 表示的是盘面中的位置）

现在我们演示下怎么获取对应feature的分数：

首先按照上面的index取出对应位置的值，（比如位置0的值是1，位置4的值是0，位置8的值是1，位置9的值是8…） 这样我们就能获取到这个feature对应的是{1, 0, 1, 8, 2, 3}，其实在这一步feature就已经提取完成了，但是这种方式找feature的时候效率会比较低，最好的方式当然是把{1, 0, 1, 8, 2, 3}这样的东西编码成一个数字，feature存在一个数组里面，这样通过key/value的方式查找效率最高。所以我们要考虑编码的方式。

前面提到过2584每一格最大可能是2178309（对应数列的第32个数），最简单的做法是把这6个数{1, 0, 1, 8, 2, 3}看成是一个32进制的数，然后转换成十进制作为查找feature值的键，首先把{1, 0, 1, 8, 2, 3}换成fibonacci数列对应的索引，改成{1, 0, 1, 5, 2, 3}，然后当做6位32进制数，换算成十进制结果是：$ 1 * 32^5 + 0 * 32^4 + 1 * 32^3 + 5 * 32^2 + 2 * 32^1+ 3 = 33592387 $，之后我们就可以在表示这个feature的数组中通过索引33592387找到对应feature的数值了。

前面的feature只是一个举例，根据这篇paper：Multi-stage temporal difference learning for 2048-like games，类似这种游戏feature应该选择32个，具体可以参照下图：

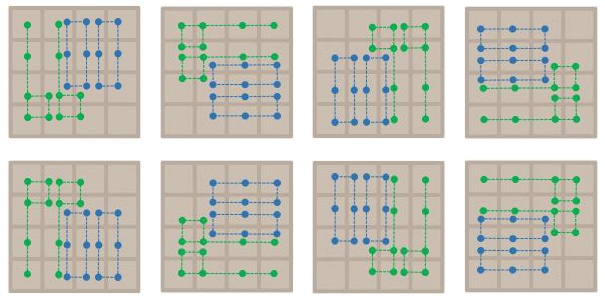
20171127_1

在paper中提到的是把左上角那幅图的feature旋转对称，其实就是做出了很多不同的feature，这八幅图的索引都是由左上到右下是从0到15，取feature的方式跟之前一样。把这32个feature编号从0到31，每个盘面的估值就是32个feature的估值相加。

merge index

接下来只需要考虑最后一个问题了，就是电脑内存。现在每个feature有6个格子，每个格子32中可能，所以我们需要一个很大很大的数组来存这个东西，前面提到过每个feature通过查数组（这个数组记成一个变量weight，长度为 $ 32^6 $ ）得到，假设32个feature分别是 $ f_0, f_1, …, f_{31} $ ，很自然的把这些feature装在一个长度为32的数组或者向量里面。把这个庞大的东西记做变量weights，由于weight这里我们用float来存，所以是一个float型的数组或者向量，一个weights又包含了32个weight。所以weights的大小是：$ 32（weights中weight的个数） * 32^6（每个weight的长度） * 32bit （一个float占32bit） = 1099511627776bit = 128GB $ 显然这个值已经超出了我们一般计算机的内存大小。

所以我们要考虑怎么压缩这个内存，一个想法就是比较大的方块不太容易出现，就算出现了对待他们的策略应该也是类似的，因此在n-tuple中区分他们会比较浪费空间。比如一个盘面的第一个feature是 { 10, 1, 3, 23, 4, 2}，另一个盘面跟这个几乎一样，只是23这个格子变成了24，所以它的第一个feature是 { 10, 1, 3, 24, 4, 2}，这时候我们应该就会觉得这两个feature几乎是一样的啊，得分也应该差不多吧，为了节省内存干脆就把他们当做一个feature好了。

从另外一个角度想，索引出现到24，意味着盘面上的数字已经到了75025，这个数其实已经很难出现了，因为一般情况下游戏很难玩到出现这个数字，我们把这个数字当做是23（fibonacci数列中对应46368）其实对AI最后的训练结果没有太大的影响。类似的，更大的数字更难出现，所以在我的这次实作中，设定了一个上限(MAX_INDEX)，表明游戏过程中这个数字几乎不会出现，把大于这个索引的情况都看作是这个索引。

这时候再估算一下内存的使用量（根据我的电脑内存12GB，MAX_INDEX设置为21）： $ 32 * 21^6 * 32bit = 87824507904bit \approx 10.22GB $ 刚好略小于12G，加上其他的运行开销勉强可以跑这个AI了。

实作代码

这次的project是在之前的基础上让AI自己具备学习能力，第一次的project每次是从上下左右滑动随机选一个可以滑动的动作。这次就要根据上面提到的理论来优化，使AI具备学习能力，在一段时间后有更好的效果。

weight.h

这个文件就是前面说到的数组，也可以理解成表格，就是根据盘面的feature查到当前这个feature的估值，只是在这个基础上增加了读写操作以及内存不够的时候会报错。这部分的代码是助教提供的，印象中没有做修改，里面的内容也不太多，稍微看看就好。

不过当时写的时候有个地方卡了一晚上，这里面出于效率的考量禁止使用拷贝构造函数。

weight(const weight& f) = delete;
weight& operator =(const weight& f) = delete;

导致的问题是后面我想把32个weight放到weights里面去的时候报错了

// initialize the n-tuple network
const long feature_num = MAX_INDEX * MAX_INDEX * MAX_INDEX * MAX_INDEX * MAX_INDEX * MAX_INDEX;
for(int i = 0; i < TUPLE_NUM; i++){
    // weight temp(feature_num);
    // weights.push_back(temp);
    weights.push_back(weight(feature_num));
}

注释掉的这个写法是错误的，原因就是用到了拷贝构造函数，而这个函数在助教的代码中被显式的禁用了，所以应该改成现在的这个写法。具体这么做的好处可以查看搜一下禁用拷贝构造函数或者右值引用。

take_action

现在考虑在轮到玩家选择动作的时候应该怎么选择的问题。根据前面提到过的，我们现在有办法知道选择动作之后下一个盘面的好坏，因此可以直接在应对当前盘面的时候在脑海中虚拟四个相同的盘面，然后分别执行上下左右四个不同的操作，把这一步得到的reward和下一个盘面的估值相加，直接选取最大的那个动作就行了。

virtual action take_action(const board& before) {
    // select a proper action
    int best_op = 0;
    float best_vs = MIN_FLOAT;
    board after;
    int best_reward = 0;

    // 模拟四种动作，取实验后盘面最好的动作作为best
    for(int op: {3, 2, 1, 0}){
        board b = before;
        int reward = b.move(op);
        if(reward != -1){
            float v_s = board_value(b) + reward;
            if(v_s > best_vs){
                best_op = op;
                best_vs = v_s;
                after = b;
                best_reward = reward;
            }
        }
    }
    action best(best_op);

    return best;
}

learn_evaluation

现在要考虑怎么一步步通过之前的游戏过程让我们的估值更加准确。通过前面知道了大概的思路，但是具体实作的时候要注意一个细节，就是我们从轮到我们操作的这个state开始，到下一次轮到我们操作，中间经过了什么。

一个游戏流程可以大致看成这样：

\[... s \xrightarrow{play-take-action} s' \xrightarrow{evil-take-action} s'' \xrightarrow{play-take-action} ...\]

上图中的s和s’‘都是玩家操作之前的情况，在玩家滑动之后，游戏会随机选一个空地放一个方块。（这部分在project1的实作中都有提到）。如果用s’的反馈来评价s的好坏就会出现一个问题：假如我们要评估状态s下，各个动作的估值，我们虚拟盘面，分别执行上下左右滑动这四个动作，假设reward都是1，之后得到的盘面估值分别是 $ s’_0 = 0.2, s’_1 = 0.4, s’_2 = 0.6, s’_3 = 0.8 $ ，然后在对应的盘面上，游戏会自动放上一个随机的方块，这个时候得到的盘面估值假设分别是 $ s’‘_0 = 0.9, s’_1 = 0.4, s’_2 = 0.2, s’_3 = 0.4 $ ，这个时候大概就能看出来问题了，从s到s’这个过程是我们可以干涉的，但是后面s’到s’‘这个过程我们无能为力，我们学到的table和实际应该学到的用下面的表格表示：

  action0 action1 action2 action3
我们学到的s估值 0.2 0.4 0.6 0.8
实际应该学到的s估值 0.9 0.4 0.2 0.4

原因是在我们做出动作后，下一个我们能操作的状态应该是s’‘而不是s’，如果使用s’的估值学习我们会觉得动作3的得分最高，应该在这个时候选择动作3，但是实际执行之后发现并不是这样，这种情况下的学习效率并不太好。

所以我们可以考虑三种学习方式：

  1. 通过s’‘的信息来更新s的估值，因为这两个状态刚好是同等的（接下来就是玩家操作），对于玩家来说也就只能看到这两个状态，也比较符合直觉
  2. 现在有s’的信息，我们通过游戏放置空白位置的概率来算出s’‘的期望。比如在s执行完动作之后s’是确定的，但是游戏放置方块比较随机，如果一共有四种可能，就需要用 $ P_0 * V(s’‘_0) + P_1 * V(s’‘_1) + P_2 * V(s’‘_2) + P_3 * V(s’‘_3) $ 的信息来更新s选择的这个动作的值。但是这个方法的计算量会比较大，并且当AI学习的越长时间，游戏玩的越多局之后，对于每个状态后面的s’‘本身就是符合这个概率的，所以不太需要每次计算一遍。
  3. 通过 $ s’_{t+1} $ 的信息来更新 $ s’_t $，这个做法与第一种方法类似，用这个的好处看了paper和上课的讲义，似乎都不太能很充分的说明为什么这个做法比较好。我的理解是这个部分要跟take_action中的部分结合起来看，在那个时候我们有一个查表的动作，查表是用来估算s’的状态，虽然s和s’有点类似，但是严格来讲并不应该一样，所以既然查表是为了得到s’的估值，在这里学习学到的是s’的估值会更加合理一点。

基本思路理清了就直接上代码，之前我们预留了open_episode和close_episode，刚好在一局开始和结束的时候调用这个，所以可以把学习的过程放在close_episode里面。s’在代码中对应的是after_state（代表玩家执行操作后的状态），需要注意的是最后一个终止状态是要单独拿出来考虑的，因为这时候已经没有下一步的局面的，这个状态之后游戏引擎随机放一个方块导致游戏结束，所以这个状态的reward设置为负值。其他的可以从后开始依次更新权重：

virtual void close_episode(const std::string& flag = "") {
    // train the n-tuple network by TD(0)
    train_weights(episode[episode.size() - 1].after);
    for(int i = episode.size() - 2; i >= 0; i--){
        state step_next = episode[i + 1];

        train_weights(episode[i].after, step_next.after, step_next.reward);
    }
}

void train_weights(const board& b, const board& next_b, const int reward){
    // 这个写法比之前的速度快，并且逻辑上更加说得通一点
    // 在更新weight的同时不应该由于前面几次循环中调整了weight而修改board value
    float delta = alpha * (reward + board_value(next_b) - board_value(b));
    for(int i = 0; i < TUPLE_NUM; i++){
        weights[i][get_feature(b, indexs[i])] += delta;
    }
}

void train_weights(const board& b){
    float delta = - alpha * board_value(b);
    for(int i = 0; i < TUPLE_NUM; i++){
        weights[i][get_feature(b, indexs[i])] += delta;
    }
}

load_weights 和 save_weights

这个训练往往会跑几天，万一中途或者训练完之后没有保存代价有点大，所以增加weights的读写操作，把weights这个变量写到文件中，或者从文件中读取信息给到这个变量。

virtual void load_weights(const std::string& path) {
    std::cout << "loading weights... " << std::endl;
    std::ifstream in;
    in.open(path.c_str(), std::ios::in | std::ios::binary);
    if (!in.is_open()) std::exit(-1);
    size_t size;
    in.read(reinterpret_cast<char*>(&size), sizeof(size));
    weights.resize(size);
    for (weight& w : weights)
        in >> w;
    in.close();
}

virtual void save_weights(const std::string& path) {
    std::cout << "saving weights to " << path.c_str() << std::endl;
    std::ofstream out;
    out.open(path.c_str(), std::ios::out | std::ios::binary | std::ios::trunc);
    if (!out.is_open()) std::exit(-1);
    size_t size = weights.size();
    out.write(reinterpret_cast<char*>(&size), sizeof(size));
    for (weight& w : weights){
        out << w;
    }
    out.flush();
    out.close();
    std::cout << "save weights success " << std::endl;
}

这部分代码没有太考虑不同系统的兼容性，似乎64位系统写入的weights文件就不能在32位系统上读取，不过如果系统相同问题似乎不大，我自己在Ubuntu系统训练的weights可以在windows上运行，不过我的电脑都是64位系统的。

最终效果

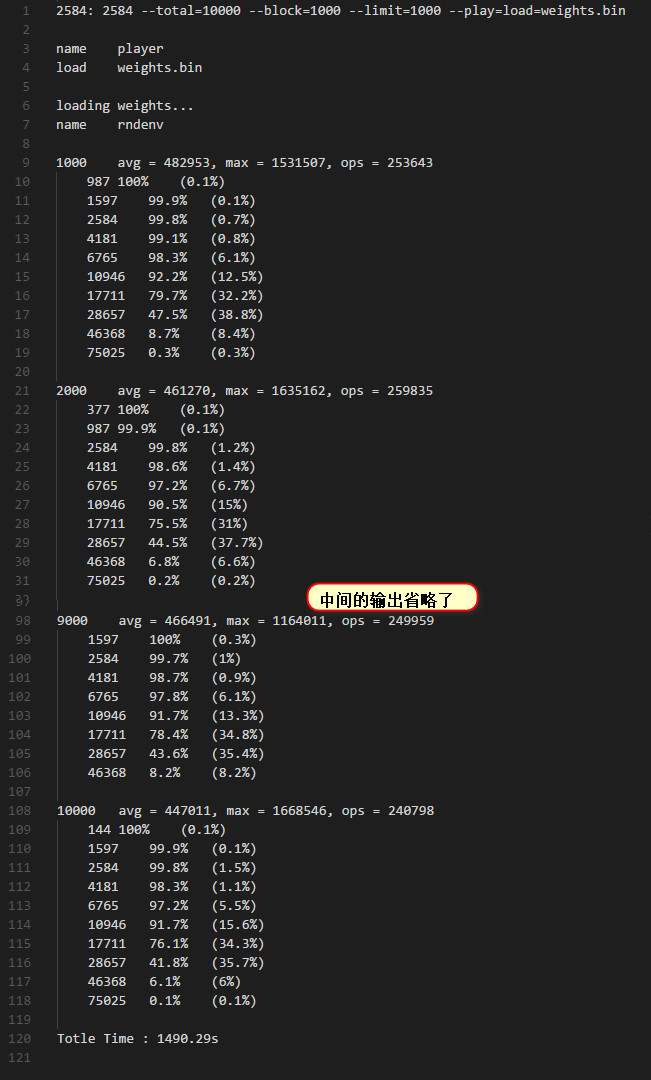
20171127_2

这好像是之前训练了两天的结果，不过不是用这台电脑训练的。从结果也能看出来，在17711前面的方块几乎能保证可以达到，但是17711后分数就一直上不去了，这是因为我们由于内存不够设置了MAX_INDEX = 21，对应的这个数值刚好就是17711，大于或者等于这个数值的方块我们的AI都没有区分，这大概也是这种方法的瓶颈。(其实感觉可以把weights这个变量存在数据库里面，不过每次跟数据库交互速度应该会比较慢，目前没有尝试这个，不过这类游戏研究的比较多的是2048，最大索引可以设置成16会方便很多)。

2584-fibonacci全部文章地址

  1. [实作]TDLearning in 2584-fibonacci (一)、搭建基础框架
  2. [实作]TDLearning in 2584-fibonacci (二)、实现TD0
  3. [实作]TDLearning in 2584-fibonacci (三)、在2x3的盘面上完成expectimax search
  4. [实作]TDLearning in 2584-fibonacci (四)、expectimax search、TCL、bitboard
  5. [实作]TDLearning in 2584-fibonacci (五)、实作evil对抗自己的AI

参考

  1. Playing Atari with Deep Reinforcement Learning
  2. Temporal difference learning of N-tuple networks for the game 2048
  3. Multi-stage temporal difference learning for 2048-like games
  4. 如何评价 C++11 的右值引用（Rvalue reference）特性？ - Tinro的回答 - 知乎