背景
DQN以及target DQN的效果已经很好了,但是人们发现了一个问题就是之前的DQN会过高估计(overestimate)Q值。一开始人们只是发现了这个事情但是并不知道这是否真的存在,以及就算存在会不会影响学习的性能,DeepMind在paper Deep Reinforcement Learning with Double Q-learning 中对这几个问题给了肯定的回答,并给出了一种简单有效的解决方案。
所以这篇paper要证明是不是真的有过高估计的问题,如果这个问题真的存在并且影响性能,要怎么解决这个问题。
Double Q-Learning
回想之前Qlearning的思路:拿到状态对应的所有动作Q值之后是直接选取Q值最大的那个动作,这会导致更加倾向于估计的值比真实的值要高。DeepMind并不是第一个发现这个问题的,早在2010年,Hasselt就针对过高估计Q值的问题提出了Double Q-Learning,他们就是尝试通过将选择动作和评估动作分割开来避免过高估计的问题。
在原始的Double Q-Learning算法里面,有两个价值函数(value function),一个用来选择动作(当前状态的策略),一个用来评估当前状态的价值。这两个价值函数的参数分别记做 $\theta$ 和 $\theta’$ 。把这个方法和原始的Qlearning做一个简单的对比,他们的target可以尝试写成下面这样:
Q-Learning:
\[\begin{align} Y^Q_t & \equiv R_{t+1} + \gamma \mathop{}\limits_a^{max}Q(S_{t+1}, a; \theta_t) \\ & \equiv R_{t+1} + \gamma Q(S_{t+1}, \mathop{}\limits_a^{argmax}Q(S_{t+1}, a; \theta_t);\theta_t) \end{align}\]Double Q-Learning:
\[Y^{DoubleQ}_t \equiv R_{t+1} + \gamma Q(S_{t+1}, \mathop{}\limits_a^{argmax}Q(S_{t+1}, a; \theta_t);\theta'_t)\]这两个公式只有最后一点点不同,在Qlearning中,我们按照当前网络的参数 $\theta_t$ 来选择下一个动作并且用一样的参数来评估对应动作的Q值,但是在DoubleQlearning中,我们用 $\theta_t$ 来决定下一个动作,但是用 $\theta’_t$ 来估计这个动作的价值。在Double Q-Learning中,这两组参数 $\theta_t$ 和 $\theta’_t$ 通过定期的交换位置来对称的更新。
估值错误(estimation error)真的存在
早在1993年,Thrun和Schwartz就发现了Q值过高估计的问题了,但是他们认为出现这个现象的原因是不足够灵活的函数近似,2010年Hasselt认为出现这个现象的原因是环境的噪声(noise)。为了弄清楚这个现象的具体原因,DeepMind在这篇paper中给出了严格的证明。
并且给出了一个定理(证明见论文的附录):

这个定理证明了任何类型的估值误差都会导致Q值增大,无论是环境噪声(environmental noise)、函数近似误差(function approximation)、非稳定性(non-stationarity)或是其他的任何原因造成的估值误差。
从定理的结论可以很容易发现学习到的估值会随着状态s对应动作数量的增大而降低下边界。
\[max_aQ_t(s, a) \ge V_*(s) + \sqrt{\frac{C}{m - 1}} \text{(其中} m \ge 2 \text{,代表状态s对应的action数量)}\]实验数据
下面这部分通过实验来直观的看出Qlearning的方式的估值真的会比真实值要大,并且Double Q-Learning的估值就会好很多。
DeepMind首先给出了一个有真实Q值的环境:假设Q值为 $Q_(s, a) = sin(s)$ 以及 $Q_(s, a) = 2 exp(-s^2)$ ,然后尝试用6阶和9阶多项式拟合这两条曲线,一共进行了三组实验,参见下面表格:
| 序号 | 目标Q值 | 使用的多项式 |
|---|---|---|
| 1 | $Q_*(s, a) = sin(s)$ | $Q_t(s, a) = \sum^6_{i=0}w_ix^i$ |
| 2 | $Q_*(s, a) = 2 exp(-s^2)$ | $Q_t(s, a) = \sum^6_{i=0}w_ix^i$ |
| 3 | $Q_*(s, a) = 2 exp(-s^2)$ | $Q_t(s, a) = \sum^9_{i=0}w_ix^i$ |
这个试验中设定有十个action(分别记做 $a_1, a_2, …, a_10$ ),并且Q值只与state有关。所以对于每个state,每个action都应该有相同的true value,他们的值可以通过目标Q值那一栏的公式计算出来。此外这个实作还有一个人为的设定是每个action都有两个相邻的state不采样,比如说 $a_1$ 不采样-5和-4(这里把-4和-5看作是state的编号), $a_2$ 不采样-4和-3等。这样我们可以整理出一张参与采样的action与对应state的表格:
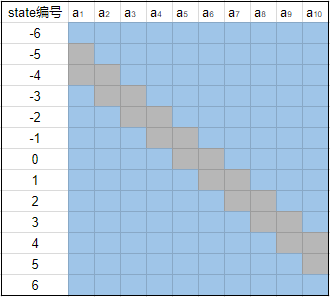
浅蓝色代表对应的格子有学习得到的估值,灰色代表这部分不采样,也没有对应的估值(类似于监督学习这部分没有对应的标记,所以无法学习到东西)
这样实验过后得到的结果用下图展示:
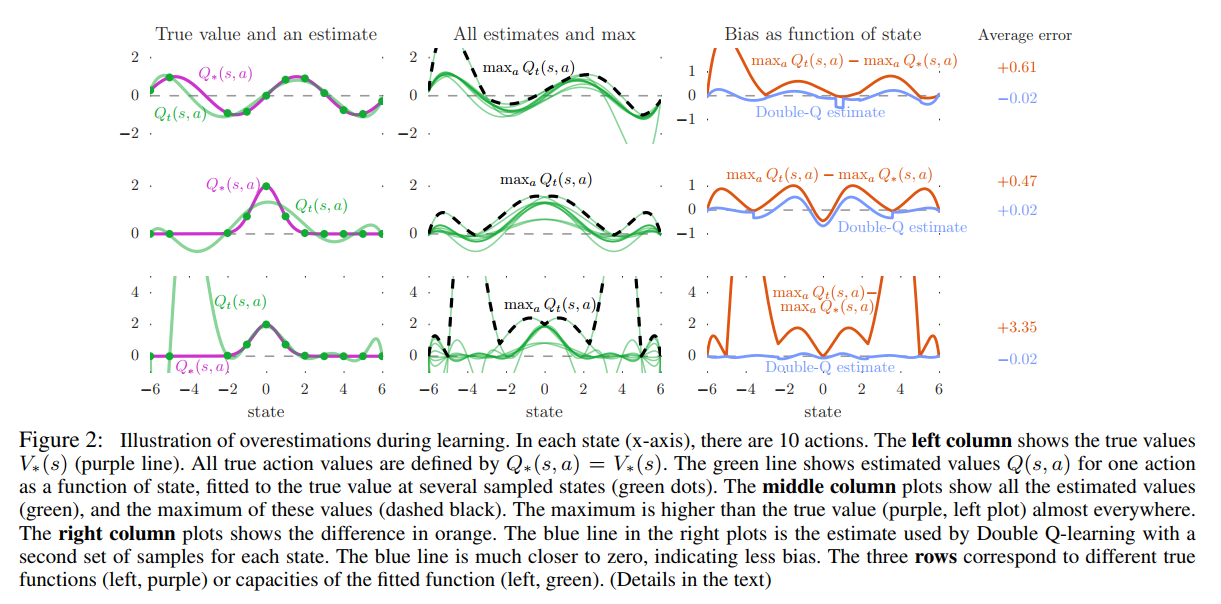
从这里面可以看出很多事情:
- 最左边三幅图(对应 $action_2$ 那一列学到的估值)中紫色的线代表真实值(也就是目标Q值,通过s不同取值计算得出),绿色的线是通过Qlearning学习后得到的估值,其中绿点标记的是采样点,也就是说是通过这几个点的真实值进行学习的。结果显示前面两组的估值不准确,原因是我们有十一个值( $s \in {-6, -5, -2, -1, 0, 1, 2, 3, 4, 5, 6}$ ),用6阶多项式没有办法完美拟合这些点。对于第三组实验,虽然能看出在采样的这十一个点中,我们的多项式拟合已经足够准确了,但是对于其他没有采样的点我们的误差甚至比六阶多项式对应的点还要大。
- 中间的三张图画出了这十个动作学到的估值曲线(对应图中绿色的线条),并且用黑色虚线标记了这十根线中每个位置的最大值。结果可以发现这根黑色虚线几乎在所有的位置都比真实值要高。
- 右边的三幅图显示了中间图中黑色虚线和左边图中紫线的差值,并且将Double Q-Learning实作的结果用同样的方式进行比较,结果发现Double Q-Learning的方式实作的结果更加接近0。这证明了Double Q-learnign确实能降低Q-Learning中过高估计的问题。
- 前面提到过有人认为过高估计的一个原因是不够灵活的value function,但是从这个实验结果中可以看出,虽然说在采样的点上,value function越灵活,Q值越接近于真实值,但是对于没有采样的点,灵活的value function会导致更差的结果,在RL领域中,大家经常使用的是比较灵活的value function,所以这一点的影响比较严重。
- 虽然有人认为对于一个state,如果这个state对应的action的估值都均匀的升高了,还是不影响我们的决策啊,反正估值最高的那个动作还是最高,我们选择的动作依然是正确的。但是这个实验也证明了:不同状态,不同动作,相应的估值过高估计的程度也是不一样的,因此上面这种说法也并不正确。
Double DQN
上一节已经通过理论和实践证明了,过高估计是真的存在,并且影响很严重。因此自然而然我们就会寻求一个解决方案来避免这个问题,或者是降低这个问题带来的影响。
DeepMind又针对这点给出了他们的解决方案:Double DQN
大致的思路其实跟前面提过的Double Q-Learning类似,下面给出Double DQN的target公式,并且与前面出现过的Q-Learning和Double Q-Learning公式进行对比:
Q-Learning:
\[Y^Q_t \equiv R_{t+1} + \gamma Q(S_{t+1}, \mathop{}\limits_a^{argmax}Q(S_{t+1}, a; \theta_t);\theta_t)\]Double Q-Learning:
\[Y^{DoubleQ}_t \equiv R_{t+1} + \gamma Q(S_{t+1}, \mathop{}\limits_a^{argmax}Q(S_{t+1}, a; \theta_t);\theta'_t)\]Double DQN:
\[Y^{DoubleDQN}_t \equiv R_{t+1} + \gamma Q(S_{t+1}, \mathop{}\limits_a^{argmax}Q(S_{t+1}, a; \theta_t);\theta^-_t)\]细心地同学已经看出来了,Double DQN和Double Q-Learning的target公式只有最后一个 $\theta$ 的上标不一样。
不过这只是公式层面上的不同,之所以标记成不一样的上标是因为他们的更新第二个网络的方式不同:在Double Q-Learning中,这两组参数 $\theta_t$ 和 $\theta’_t$ 通过定期的交换位置来对称的更新。而在Double DQN中,目标网络的参数 $\theta$ 更新方式是与原有的DQN保持一致,只是多了另外一个网络的参数,这个网络更新方式是定期的将前面一个网络的参数同步过来。(从原有的交换位置对称更新,变成了定期将一边的参数复制到另一边进行同步)
在Atari游戏上的实作
跟之前的两篇paper一样,提出了一种新的思路就在Atari这种理想的RL环境中验证一下效果。任然是所有的游戏都使用同一套超参数,同一套神经网络。有一点不同的是,这次的神经网络架构与之前的略微不同。对比如下图:
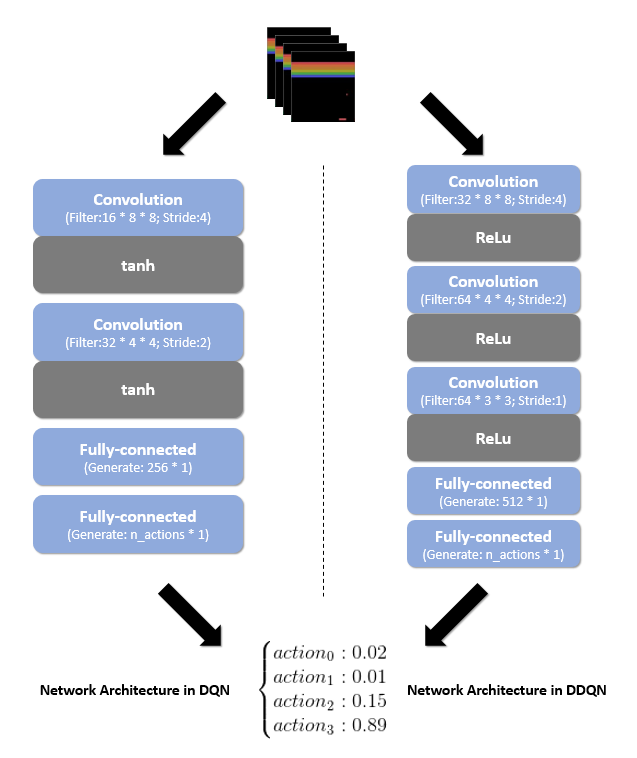
这次着重观察了DQN和Double DQN(下面简称DDQN)在六个游戏中的表现,并且得到了这样的实验结果:
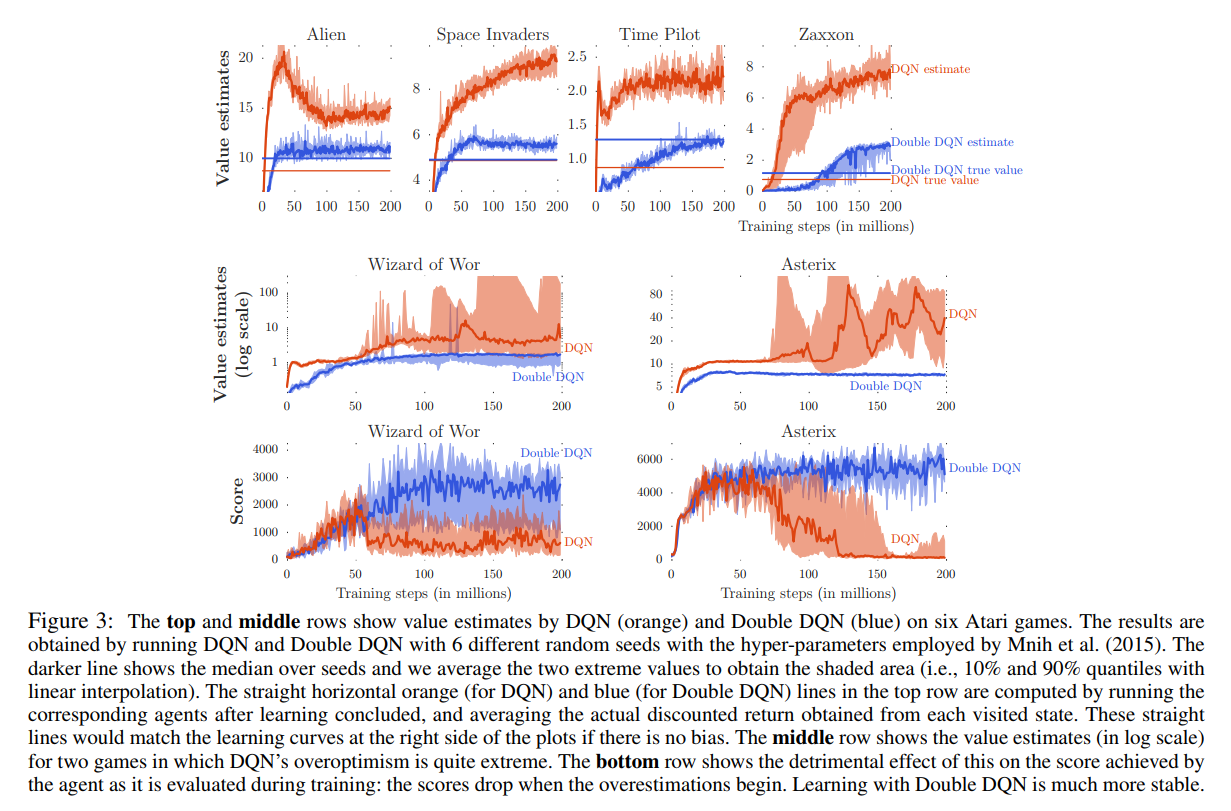
注意到上面四张图中有true value,但是对于Atari游戏来讲,我们很难说某个状态的Q值等于多少,于是DeepMind想到了一个代替方案:拿到已经学好的游戏策略,按照这个策略去跑几次游戏,然后我们就能知道一个游戏中积累的reward,就能得到平均的reward作为true value了。
如果没有过高估计的话,收敛之后我们的估值应该跟真实值相同的(每个图的曲线应该跟直线在最右端重合),但是从图中看出,大部分情况下并不是这样,这又一次证明了过高估计确实不容易避免,但是我们可以看出,针对这个问题,DDQN确实比DQN做的要好很多。
除此之外,通过Wizard of Wor和Asterix这两个游戏可以看出,DQN的结果比较不稳定。这也进一步证明了过高估计会影响到学习的性能。但是在之前有人认为这些不稳定的问题是off-policy learning固有的,于是这篇paper中将DDQN的结果摆在了一起,DDQN跟DQN一样是off-policy learning,但是在这两个游戏中表现的更加稳定,因此不稳定的问题的本质原因还是对Q值的过高估计。
随后为了验证学到的策略的质量以及算法是否稳定,他们用下面三种方式在不同Atari游戏上进行了对比:
- 之前的DQN
- 完全采用之前DQN的超参数(hyper-parameter),只是改成用DDQN(查看DDQN在减小过高估计这一点上比DQN的优势)
- 调整第二种方法上的超参数,发挥DDQN更大的性能
整体的实验结果不出所料,第三种的结果比前面两种都要好。
更进一步的,他们为了证明算法的稳定性,采用了不同的时间点开始切入学习(比如人们先玩30分钟在让AI开始学习),发现DDQN的结果更加稳定,并且DDQN的解并没有利用到环境的相关特性。
总结
总结一下这篇paper的内容:
- 他们证明了在很多的问题中,Qlearning都会导致过高估计的问题。
- 通过在Atari游戏中的实验,他们发现这个问题比之前人们预想的都要严重。
- 他们证明了使用Double Q-Learning能减少这类问题的影响,导致结果更加稳定以及可信。
- 他们提出了DDQN,可以很方便的在原有DQN上进行修改,直接使用现成的深度神经网络架构,并且不需要额外的参数。
- DDQN在Atari 2600领域获得了更好的成果。
