• 背景
• 理论基础
  • 迭代公式推导
• 算法详解
  • experience replay机制(off-policy)
  • 算法过程
• 实验
  • 图像预处理
  • 选择模型的输入与输出
  • 神经网络的搭建
  • 实验过程
  • frame-skipping technique
  • 结果分析
  • Q值可视化
  • 评估
• 参考

背景

这篇paper是现在Deep Reinforcement Learning的开山之作，DeepMind尝试将CNN与RL结合，并且把这个做法用在了7个Atari游戏中，有6个游戏最终的效果比以往的方法要好，其中有三个还超过了人类玩家的水平。

在这篇paper之前，人们尝试将RL用在类似游戏中的时候都需要手动提取feature，但是人工提取的feature必然涉及到人类已有的知识，比如说对于打砖块(Breakout)游戏，人类要想办法提取到球和挡板的位置，以及剩下方块的位置，把这些东西告诉算法，算法根据这些信息判断挡板现在是应该往哪边移动或者是保持静止。

乍一看这种方式似乎没有什么问题，因为人类玩打砖块似乎也是要提取到这些信息，根据这些信息进行判断该怎么操作。但是仔细想想就会发现这种方式存在一些局限性：

• 针对不同的游戏需要提取不一样的feature。对于打砖块可以提取上面提到的球的位置，挡板的位置，剩下砖块的位置等。但是换了一个游戏，比如flappy bird，你就需要花很多时间想办法获取小鸟的位置以及各个水管的位置等。这会导致一个游戏的算法不能很好的应用在另一个游戏上，没有实现通用性。
• 提取的feature很复杂的时候，会造成存储或计算的瓶颈（状态空间过大）。还是以打砖块为例，提取游戏中的feature的时候，如果直接提取位置，假设以像素作为坐标表示，我们需要提取的feature就会由很多坐标组成，然后每个坐标又有很多情况，这样就会造成我们提取的feature可能的情况太多，使用传统的Qlearning的话需要为每个state估计Qvalue，直接造成计算量过大，并且可能无法存下这么巨大的Qtable。
• 提取的feature不一定准确。为了防止提取的feature过于复杂，我们往往会对feature进行压缩，找出关键性的feature喂给RL模型进行学习。比如flappy bird中我们可以把小鸟的位置和各个水管的位置改成小鸟和下一个水管的相对位置等。这样虽然可以将复杂的feature简化，从而减小状态空间的大小。但是存在的问题是我们提取到的feature不一定准确。我们提取feature的时候往往受限于自身经验，对于简单问题也许还好，只要仔细并且实验几次往往不会有问题，但是对于复杂的问题，人类经验显得不足或者是错误的时候，这样提取的feature肯定不会达到很好的效果。

因此这篇paper提出了一种新的方式，直接将整个游戏画面作为模型的输入，让模型自己去考虑应该提取什么样的feature，甚至于最后具体学到的是什么feature其实我们也并不关心，只需要模型能在各种状态(state)下做出正确的动作(action)就行了。

理论基础

原始的Qlearning算法可以想象有一个表格来存储每个状态下对应action的Q值，决策阶段会根据当前状态去表中查Q值，选择Q值最大的那个动作。但是由于前面提到的，人工提取feature可能不准确，并且造成局限性不能迁移到其他游戏中，所以直观的方式就是直接将原始游戏画面代表当前状态。这样省掉了人工提取feature的过程，理论上也一定能学到东西，因为人类玩家获取到的就是这样的游戏画面并且能玩出不错的分数。

选择了将游戏画面作为模型输入就解决了前面提到的第一个和第三个问题，接着要处理状态空间过大的问题。虽然游戏画面的像素点很多，每个像素又有 $ 256^3 $ 种可能（Atari游戏每个像素只有128种可能），但是像素点之间是有关联的，所以不需要独立看每个像素点的情况。刚好CNN能很好的处理这些问题，所以这篇paper的想法是搭建CNN模型处理游戏画面，模型输出当前画面下各个动作的Q值。接下来想办法使这个模型的输出更加准确就行了。

让模型更加准确可以考虑使用大量的数据进行迭代，在RL领域比较方便的就是数据可以通过不断的游戏过程得到，在这篇paper中采用了off-policy的策略，将游戏过程存入replay memory里面（包含当初做决策的状态(state, $ s_t $)，当初选择的动作(action, $ a_t $)，环境给出的得分(reward, $ r_t $)和做出动作后的那个状态(state’, $ s_{t+1} $），在学习的过程中就是从replay memory中选取一部分样本喂给迭代算法，不停的迭代模型中的参数，让模型的输出更加准确。

迭代公式推导

目前已经有了大致的框架，就差一个迭代算法让模型的输出更加准确了。现在回想一下，我们需要的模型输出是Q值，Q值代表的意思是当前状态下对应动作的好坏。对于最终的状态，一个动作导致游戏结束当然就很好理解了，Q值就是游戏这个时候给出的reward，reward越高说明这个状态下选择的动作越好，reward越低说明这时候选择的动作越差。但是对于一个动作后游戏没有结束，我们就不能仅仅通过reward来判断这个Q值的大小了，比如说某个时候你发现地面上有个食物，往前一步就能获得食物（有一个正的reward），但是获得食物的同时你发现这是个陷阱，会直接导致游戏结束，当然就不能说发现食物那个状态下往前移动的这个动作Q值很高。

在这个情况下，DeepMind做出了第一个假设，这个游戏的过程是一个马尔科夫决策过程（MDP）：下一个状态仅仅取决于当前的状态和当前的动作。这个假设就将过去剔除了出去，当前的Q值不再取决于过去发生了什么，也不取决于是从哪个状态通过哪个动作到达的现在的状态。因此我们可以假设目前状态在未来的影响( $ R_t $ )是未来所有状态下reward的总和：

\[R_t = r_t + r_{t+1} + r_{t+2} + ... + r_T\]

但是根据经验，不同时间的选择其实对未来造成的影响是不一样的，时间越远造成的影响会越小。换句话说现在的回报不应该表示成未来所有reward的总和，而应该是在未来的reward上乘以一个衰减系数。所以上面的公式应该进行一些修改：

\[R_t = r_t + \gamma * r_{t+1} + {\gamma}^2 * r_{t+2} + ... + {\gamma}^{T-t} * r_T\]

对这个公式进行一些改动：

\[\begin{align} R_t & = r_t + \gamma * r_{t+1} + {\gamma}^2 * r_{t+2} + ... + {\gamma}^{T-t} * r_T \\ & = r_t + \gamma * (r_{t+1} + {\gamma} * r_{(t+1)+1} + ... + {\gamma}^{T-(t+1)} * r_T) \end{align}\]

到了这一步，DeepMind做出了另一个重要的假设：每个时刻在未来的回报 $ R_t $ 满足Bellman Equation：在一个序列求解的过程中，如果一个解的路径是最优路径，那么其中的每个片段都是当前的最佳路径。

简单来讲就是如果我们希望t时刻在未来的影响达到最好，在t时刻做出选择之后，t+1时刻在未来的影响也要最好。

把理想状态下对未来最好的影响记做 $ Q^* $， $ Q^* $满足下面公式：

\[\begin{align} Q^*(s_t, a_t) & = R_t \\ & = r_t + \gamma * (r_{t+1} + {\gamma} * r_{(t+1)+1} + ... + {\gamma}^{T-(t+1)} * r_T) \end{align}\]

根据Bellman Equation，在 $ s_{t+1} $状态下，需要使Q值最大的动作才能达到 $ Q^*(s_t, a_t) $ ，所以进一步整理公式：

\[\begin{align} Q^*(s_t, a_t) & = r_t + \gamma * (r_{t+1} + {\gamma} * r_{(t+1)+1} + ... + {\gamma}^{T-(t+1)} * r_T) \\ & = r_t + \gamma * max_{a'} Q(s_{t+1}, a') \end{align}\]

$ max_{a’} Q(s_{t+1}, a’) $ 表示状态 $ s_{t+1} $ 下所有动作中最大的Q值。

至此我们就可以根据下一个状态推导出现有状态理想情况下的Q值了。现在我们来整理一下模型参数的迭代过程：目前我们有一个状态 $ s_t $，将这个状态喂给模型得到了每个动作下对应的 $ Q_t $ 值，我们选取了Q值最大的动作得到了reward和下一个状态 $ s_{t+1} $。有了下一个state我们又可以通过模型得到所有动作对应的 $ Q_{t+1} $ 值。由上面公式可以得到 $Q_t^{\star} = r_t + \gamma * Q_{t+1}$ ，理论上 $Q_t^{\star} = Q_t$ ，但是由于模型一开始并不是完美的，得到的Q值也会跟理想情况有差距，所以才需要不停的迭代。我们可以用实际值和理想值之间的差值作为loss function，并通过大量样本最小化这个loss function来完善模型。

最终的算法如下：

算法详解

experience replay机制(off-policy)

experience replay机制是在agent每一步选择之后把这次的经验 $ e_t = (s_t, a_t, r_t, s_{t+1}) $ 存在一个集合(replay memory)中( $ D = e_1, e_2, …, e_N $ )，集合的大小是固定的，每次满了之后有新的经验需要进来时就把最旧的经验剔除出去。然后在迭代的过程中是直接从集合中随机选取固定数量的经验作为训练样本(mini-batch)优化神经网络。具体优化措施这篇paper中使用的是RMSProp使loss function下降

其实用其他的梯度下降算法也类似，只有收敛速度跟最后结果可能有细微的差别，具体可以根据需要补充相关的机器学习课程，可以参考这个课件中的介绍

使用experience replay的好处有：

• 每一步的经验可能在更新神经网络权重的时候被使用很多次，让数据使用更有效率。
• 由于连续的样本之间有很强的关联性，使用连续的样本比较没有效率。而随机的样本能打破这种关联
• 如果不使用experience replay而采用on-policy的机制，当前的参数就决定了下一个训练样本，我们又要根据这个样本训练我们的参数，这样很容易导致训练过程中不愿意看到的反馈回路(feedback loop)，结果可能导致收敛到了一个局部最优解甚至是结果产生灾难性的偏移。

算法过程

现在回过头看下带有经验回放的DQN(Deep Q-learning with Experience Replay)

一开始的时候初始化replay memory的容器D，大小为N，然后随机初始化神经网络的权重。接下来开始M局游戏，在每局游戏的开始拿到初始状态 $ s_1 $ 并且进行预处理得到 $ \phi_1 $ 。

然后在每一步操作，以一定的概率 $ \epsilon $ 选择一个随机的动作，其他时候选择当前状态下Q值最大的动作。这时候就可以得到 $ r_t $ 和 $ s_{t+1} $，并对 $ s_{t+1} $ 的图像进行处理得到 $ \phi_{t+1} $ 。

将这个动作相关的信息( $ \phi_t, a_t, r_t, \phi_{t+1} $ )存储到replay memory中，并且从D中随机选取minibatch( $ \phi_j, a_j, r_j, \phi_{j+1} $ ), 按照下面公式计算理论上的Q值：

\[y_j = \begin{cases} r_j, & \text{for terminal $ \phi_{j+1} $ } \\ r_j + \gamma max_{a'} Q(\phi_{j+1}, a'; \theta), & \text{for non-terminal $ \phi_{j+1} $ } \end{cases}\]

以及通过减少 $ loss function = (y_j - Q(\phi_j, a_j; \theta))^2 $ 来优化神经网络的权重

实验

图像预处理

Atari游戏的原始画面是210 * 160像素的图案，每个像素可以选择的颜色有128种，首先对原始图像进行预处理，大小缩放成110 * 84像素，并且转成灰度图像。由于后面模型中的卷积操作一般需要输入的图像是正方形，所以还需要将图像切成84 * 84像素大小，保留主要的游戏画面。最终输入给模型的是由四帧处理过的图像组成的一个状态$\phi$

选择模型的输入与输出

有许多思路可以得到当前状态每个动作对应的Q值，比如说可以将状态和每个动作都作为模型的输入，输出的结果就作为当前的Q值，但是这种做法的缺点很明显，我们对应同一个状态，需要把每个动作都与这个状态一起喂给模型，最终才能得到这个状态下所有动作对应的Q值，这个过程需要模型拿不同的action跑很多次。所以这篇paper中的做法是采用只有当前的状态作为模型的输入，输出的是当前状态下所有动作对应的Q值，这样针对每个状态只需要跑一次模型就可以了，可以节省计算量。

神经网络的搭建

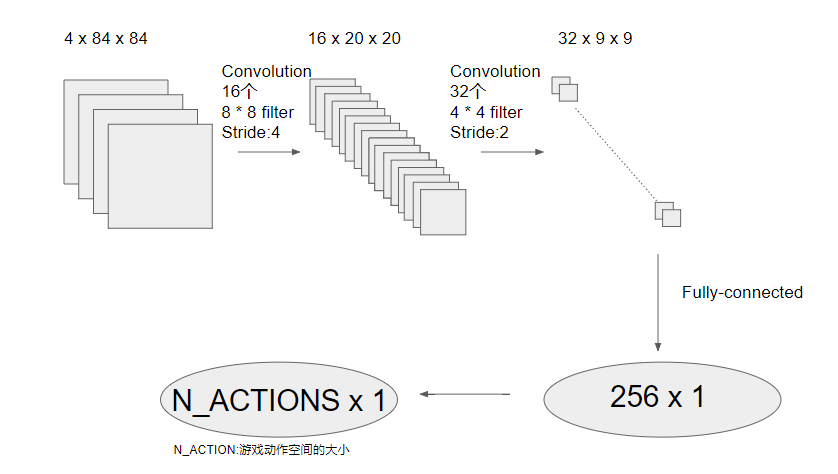
根据paper画出的神经网络架构图如下，是两个卷积层加上两个全连接层

每次卷积之后会加一个非线性层（激活函数），目前用的比较多的是ReLU，但是这个paper中没有提到使用的是什么函数，根据这部分的参考文献推测可能是tanh

实验过程

为了证明这种做法的稳定性以及通用性，DeepMind用同一个网络架构，同样的学习算法，甚至选择同样的网络的超参数(hyperparameters)实作7个Atari游戏(Beam Rider, Breakout, Enduro, Pong, Q*bert, Seaquest, Space Invaders)。他们仅仅是将这7个游戏中的reward进行了一些修改：所有的正reward改成1，负的reward改成-1，其他的时候是0。这样做的目的是为了让不同的游戏保持同样的学习率(learning rate)，同时也能在评估效果的时候采用同样的标准。

其他参数设置：

• 梯度下降算法： RMSProp
• minibatch大小： 32
• $\epsilon-greedy$中$\epsilon$的选择： 前1,000,000帧画面，$\epsilon$线性的从1到0.1，随后保持0.1不变
• 总训练量： 10,000,000帧画面
• replay memory：最近1,000,000帧画面

frame-skipping technique

在试验中，DeepMind并不是每帧画面都会观察并且进行相应的动作，而是每kth帧画面观察一次并且做出动作变化，其他时候就维持最后的一个动作不变。这样的好处是在同样的时间内学到更多新的游戏状态。最后他们除了Space Invaders游戏中k选择3之外（因为这个游戏k设置成4会由于闪烁造成激光看不见），其他游戏的k都选择为4。

结果分析

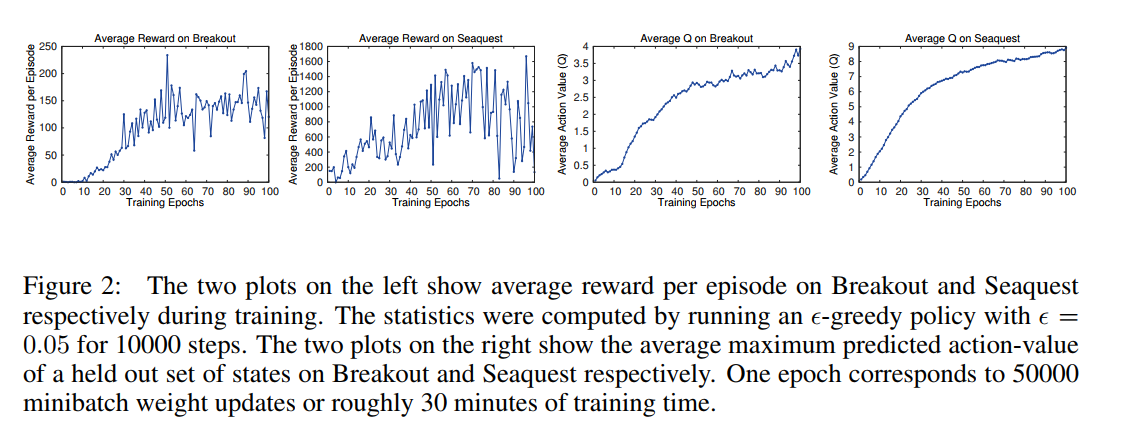
不同于监督学习，强化学习并没有一个很好的评量标准，原本DeepMind打算采用不同训练时间下平均得分作为衡量标准，但是发现平均得分的震荡幅度有点大（如下图中最左边的两个图），分析原因推测是小的权重变化会导致选择动作的策略不同，策略的改变导致游戏过程中遇到的状态的分布有很大的变化，所以导致得分不稳定。因此最后选择平均Q值作为评估标准，下图中右边两幅图中也可以看出Q值比较平滑的上升。这表明虽然缺乏理论的证明，但是这种做法确实能用强化学习的信号训练大型的神经网络并且收敛。

Q值可视化

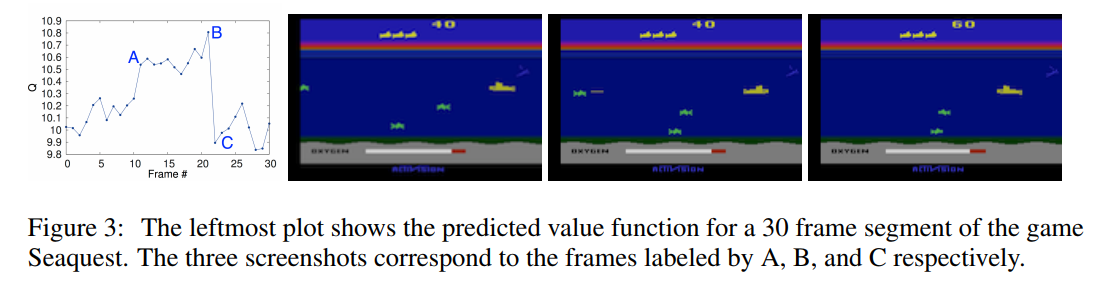
下图中的实验简单描述了Q值直观上的意义。游戏截图中的第一幅图表明左侧有一个新的敌人出现，这时候网络给出的估值瞬间飙高；第二幅图表示玩家子弹快要打中敌人了，如果打中就会产生一个新的reward，这时候的估值再次升高；第三幅图是子弹打到敌人已经拿到reward后，网络给出的估值又回到了原先敌人没有出现的地方附近。

评估

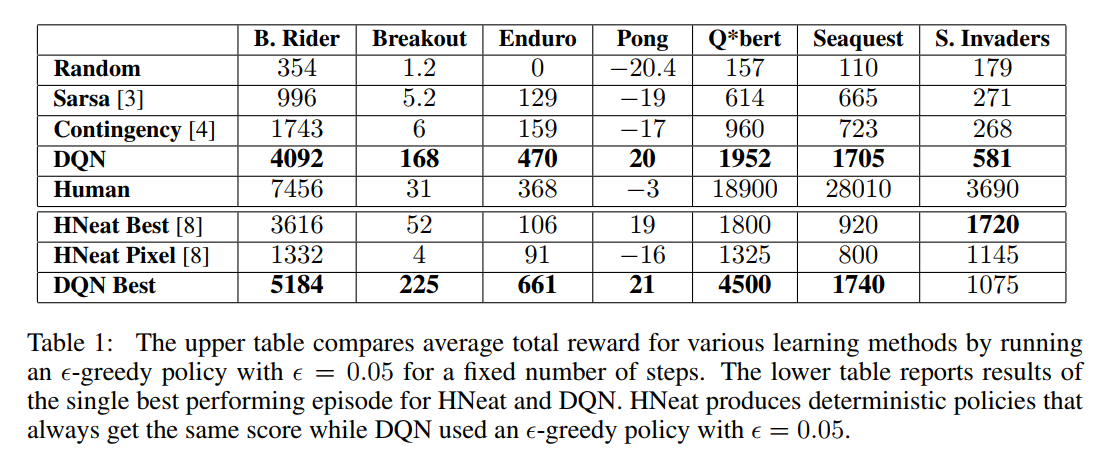
此前也有一些算法在尝试解Atari的问题，其中一个叫做Sarsa方法使用Sarsa算法学习手动提取的特征，Contingency方法与Sarsa方法类似，但是有部分的学习过程。这两个方法都在手动提取特征的同时分离出了背景（有点类似把128种颜色作为128个图层分开，然后标注每种颜色代表什么），虽然对于Atari游戏，通常不同的颜色对应不同类别的物体，这种方式效果还不错。但是作为对比，DeepMind没有采用这个方式，而是需要神经网络自己学习分离背景和游戏物体。

此外，他们还比较了人类玩家和不同算法的得分情况。除了上面介绍的算法之外还有随机的选择动作。对比结果在下面列表所示，其中HNeat Best代表人工标注屏幕上物体的位置和类别的结果，HNeat Pixel代表使用8个特别的颜色做出八个图层，然后标注每个图层代表的类别的结果。

参考

1. Playing Atari with Deep Reinforcement Learning
2. List of video game console palettes
3. 马尔可夫性质 - 维基百科，自由的百科全书
4. Stanford University CS231n: Convolutional Neural Networks for Visual Recognition
5. Paper Reading 1 - Playing Atari with Deep Reinforcement Learning - songrotek的专栏 - 博客频道 - CSDN.NET
6. What is the Best Multi-Stage Architecture for object Recognition